题目内容
1. 如图,已知A是双曲线y=$\frac{2}{x}$(x>0)上一点,过点A作AB∥y轴,交双曲线y=-$\frac{1}{x}$(x>0)于点B,过点B作BC⊥AB交y轴于点C,连接AC,则△ABC的面积为$\frac{3}{2}$.
如图,已知A是双曲线y=$\frac{2}{x}$(x>0)上一点,过点A作AB∥y轴,交双曲线y=-$\frac{1}{x}$(x>0)于点B,过点B作BC⊥AB交y轴于点C,连接AC,则△ABC的面积为$\frac{3}{2}$.
分析 过A作AE⊥y轴于E,设AB交x轴于D,得到四边形ABCE是矩形,根据反比例函数系数k的几何意义即可得到结论.
解答 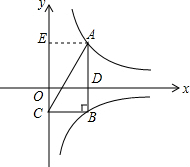 解:过A作AE⊥y轴于E,设AB交x轴于D,∵AB∥y轴,
解:过A作AE⊥y轴于E,设AB交x轴于D,∵AB∥y轴,
∴AB⊥x轴,
∵BC⊥AB,
∴四边形ABCE是矩形,
∵A是双曲线y=$\frac{2}{x}$(x>0)上一点,
∴S四边形ADOE=2,
∵B在双曲线y=-$\frac{1}{x}$(x>0)上,
∴S四边形BDOC=1,
∴△ABC的面积=$\frac{1}{2}$S矩形ABCE=$\frac{3}{2}$;
故答案为:$\frac{3}{2}$.
点评 本题考查了反比例函数系数k的几何意义,矩形的面积,熟练掌握反比例函数系数k的几何意义是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.一个口袋中有红球、黄球共20个,这些除颜色外都相同,将口袋中的球搅拌均匀,从中随机摸出一球,记下颜色后再放回口袋,不断重复这一过程,共摸了200次,发现其中有161次摸到红球.则这个口袋中红球数大约有( )
| A. | 4个 | B. | 10个 | C. | 16个 | D. | 20个 |
13.小亮根据取x的值为:1.1,1.2,1.3,1.4,1.5时,代入x2-12x-15求值,估算一元二次方程的解( )
| x | 1.1 | 1.2 | 1.3 | 1.4 | 1.5 |
| x2+12x-15 | -.59 | 0.84 | 2.29 | 3.76 | 5.25 |
| A. | 1.1<x<1.2 | B. | 1.2<x<1.3 | C. | 1.3<x1.4 | D. | 1.4<x<1.5 |
11.设a,b是方程x2+x-2015=0的两个根,则a2+2a+b的值为( )
| A. | 2014 | B. | 2015 | C. | 2016 | D. | 2017 |

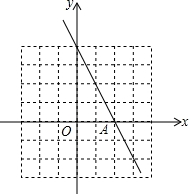 已知一次函数y1=kx+b与函数y=-2x的图象平行,且与x轴的交点A的横坐标为2.
已知一次函数y1=kx+b与函数y=-2x的图象平行,且与x轴的交点A的横坐标为2. 已知:如图,△ABC≌△DFE,若∠A=60°,∠E=90°,DE=6cm,则AB=12cm.
已知:如图,△ABC≌△DFE,若∠A=60°,∠E=90°,DE=6cm,则AB=12cm.