题目内容
17. 如图,已知BD,CE分别是∠ABC和∠ACB的平分线,∠DBC=∠ECB.
如图,已知BD,CE分别是∠ABC和∠ACB的平分线,∠DBC=∠ECB.(1)猜想∠ABC和∠ACB的大小关系,并说明理由;
(2)若∠DBC=35°,求∠A的度数.
分析 (1)根据BD与CE分别是∠ABC和∠ACB的平分线得出∠ABC=2∠DBC,∠ACB=2∠ECB,由∠DBC=∠ECB即可得出结论;
(2)由(1)得出∠ACB=∠ABC=2∠DBC=70°,再由三角形内角和定理即可得出结果.
解答 解:(1)∠ABC=∠ACB;理由如下:
∵BD与CE分别是∠ABC和∠ACB的平分线,
∴∠ABC=2∠DBC,∠ACB=2∠ECB,
又∠DBC=∠ECB,
∴∠ABC=∠ACB.
(2)由(1)得:∠ACB=∠ABC=2∠DBC=70°,
∴∠A=180°-70°-70°=40°.
点评 本题考查了三角形的角平分线、三角形内角和定理;熟练掌握角平分线的定义和三角形内角和定理是解答本题的关键.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
2.下列说法错误的是( )
| A. | 两点之间的所有连线中,线段最短 | |
| B. | 经过一点有且只有一条直线与已知直线平行 | |
| C. | 如果两条直线都与第三条直线平行,那么这两条直线也互相平行 | |
| D. | 经过一点有且只有一条直线与已知直线垂直 |
 如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于点D,DE⊥AB于点E,若BC=7,则AE的长为( )
如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于点D,DE⊥AB于点E,若BC=7,则AE的长为( )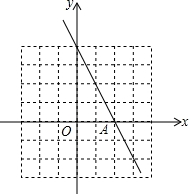 已知一次函数y1=kx+b与函数y=-2x的图象平行,且与x轴的交点A的横坐标为2.
已知一次函数y1=kx+b与函数y=-2x的图象平行,且与x轴的交点A的横坐标为2. 已知:如图,△ABC≌△DFE,若∠A=60°,∠E=90°,DE=6cm,则AB=12cm.
已知:如图,△ABC≌△DFE,若∠A=60°,∠E=90°,DE=6cm,则AB=12cm. 已知直线y=x+7与双曲线y=$\frac{k}{x}$(k≠0)的一个交点的坐标为(1,m).
已知直线y=x+7与双曲线y=$\frac{k}{x}$(k≠0)的一个交点的坐标为(1,m).