题目内容
9.二次函数y=ax2+2ax+c的图象与x轴交于(3,0),则一元二次方程ax2+2ax+c=0的一个解x1=3,另一个解x2=-5.分析 根据一元二次方程的根与系数的关系来求方程ax2+2ax+c=0的另一根即可.
解答 解:∵二次函数y=ax2+2ax+c的图象与x轴交于(3,0),则一元二次方程ax2+2ax+c=0的一个解x1=3,
∴x1+x2=-2,即3+x2=-2,
解得x2=-5.
故答案是:-5.
点评 本题考查了抛物线与x轴的交点坐标.求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标,令y=0,即ax2+bx+c=0,解关于x的一元二次方程即可求得交点横坐标.

练习册系列答案
相关题目
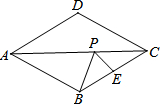 如图,在菱形ABCD中,AD=6,∠ABC=120°,E是BC的中点,P为对角线AC上的一个动点,则PE+PB的最小值为3$\sqrt{3}$.
如图,在菱形ABCD中,AD=6,∠ABC=120°,E是BC的中点,P为对角线AC上的一个动点,则PE+PB的最小值为3$\sqrt{3}$.