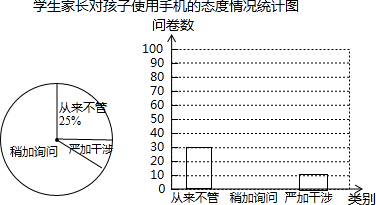
题目内容
1.已知一元二次方程x2-4x-3=0的两根为m,n,则m2-mn+n2=25.分析 由m与n为已知方程的解,利用根与系数的关系求出m+n与mn的值,将所求式子利用完全平方公式变形后,代入计算即可求出值.
解答 解:∵m,n是一元二次方程x2-4x-3=0的两个根,
∴m+n=4,mn=-3,
则m2-mn+n2=(m+n)2-3mn=16+9=25.
故答案为:25.
点评 此题考查了一元二次方程根与系数的关系,将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法.

练习册系列答案
相关题目
16.下列运算正确的是( )
| A. | (2a2)3=6a6 | B. | -a2b2•3ab3=-3a2b5 | ||
| C. | $\frac{b}{a-b}$+$\frac{a}{b-a}$=-1 | D. | $\frac{{a}^{2}-1}{a}$•$\frac{1}{a+1}$=-1 |
13. 如图,正方形ABCD的边长为2,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…按照此规律继续下去,则S2015的值为( )
如图,正方形ABCD的边长为2,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…按照此规律继续下去,则S2015的值为( )
 如图,正方形ABCD的边长为2,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…按照此规律继续下去,则S2015的值为( )
如图,正方形ABCD的边长为2,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…按照此规律继续下去,则S2015的值为( )| A. | ($\frac{\sqrt{2}}{2}$)2012 | B. | ($\frac{\sqrt{2}}{2}$)2013 | C. | ($\frac{1}{2}$)2012 | D. | ($\frac{1}{2}$)2013 |
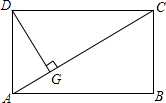 如图,在矩形ABCD中,DG⊥AC,垂足为G.
如图,在矩形ABCD中,DG⊥AC,垂足为G.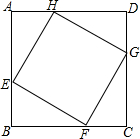 如图,正方形ABCD的边长为8cm,E、F、G、H分别是AB、BC、CD、DA上的动点,且AE=BF=CG=DH.
如图,正方形ABCD的边长为8cm,E、F、G、H分别是AB、BC、CD、DA上的动点,且AE=BF=CG=DH.