题目内容
12.在?ABCD中,M,N是AD边上的三等分点,连接BD,MC相交于O点,则S△MOD:S△COB=4:9或1:9.分析 首先根据M,N是AD边上的三等分点,判断出$\frac{DM}{BC}=\frac{2}{3}$或$\frac{DM}{BC}=\frac{1}{3}$;然后根据四边形ABCD是平行四边形,判断出AD∥BC,△MOD∽△C0B,据此求出S△MOD:S△COB的值是多少即可.
解答 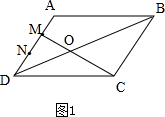 解:∵M,N是AD边上的三等分点,
解:∵M,N是AD边上的三等分点,
(1)当$\frac{DM}{BC}=\frac{2}{3}$时,如图1,
∵四边形ABCD是平行四边形,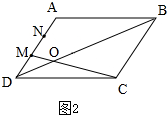
∴AD∥BC,
∴△MOD∽△C0B,
∴S△MOD:S△COB=($\frac{DM}{BC}$)2=4:9.
(2)当$\frac{DM}{BC}=\frac{1}{3}$时,如图2,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴△MOD∽△C0B,
∴S△MOD:S△COB=($\frac{DM}{BC}$)2=1:9.
故答案为:4:9或1:9.
点评 (1)此题主要考查了相似三角形的性质和应用,要熟练掌握,解答此题的关键是要明确:寻找相似三角形的一般方法是通过作平行线构造相似三角形;或依据基本图形对图形进行分解、组合;或作辅助线构造相似三角形,判定三角形相似的方法有时可单独使用,有时需要综合运用,无论是单独使用还是综合运用,都要具备应有的条件方可.
(2)此题还考查了平行四边形的性质和应用,要熟练掌握,解答此题的关键是要明确平行四边形的性质:①边:平行四边形的对边相等.②角:平行四边形的对角相等.③对角线:平行四边形的对角线互相平分.
(3)此题还考查了三角形的面积的求法,要熟练掌握,解答此题的关键是要明确:三角形的高一定时,三角形的面积和底成正比.

练习册系列答案
相关题目
17.下列运算,结果正确的是( )
| A. | m2+m2=m4 | B. | (m+$\frac{1}{m}$)2=m2+$\frac{1}{{m}^{2}}$ | C. | (3mn2)2=6m2n4 | D. | 2m2n÷$\frac{m}{n}$=2mn2 |
2. 将直尺和直角三角板按如图方式摆放,已知∠1=30°,则∠2的大小是( )
将直尺和直角三角板按如图方式摆放,已知∠1=30°,则∠2的大小是( )
 将直尺和直角三角板按如图方式摆放,已知∠1=30°,则∠2的大小是( )
将直尺和直角三角板按如图方式摆放,已知∠1=30°,则∠2的大小是( )| A. | 30° | B. | 45° | C. | 60° | D. | 65° |