题目内容
2.若-3xm+1y2016与2x2015yn是同类项,则|m-n|的值是( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 根据同类项相同字母的指数分别相同,求出m、n的值,再计算其差的绝对值即可.
解答 解:∵-3xm+1y2016与2x2015yn是同类项,
∴m+1=2015,n=2016
∴m=2014,n=2016
∴|m-n|
=|2014-2016|
=2
故选:C.
点评 本题考查了同类项的概念及绝对值的相关计算.解决本题的关键是利用同类项的定义,确定m、n的值.

练习册系列答案
相关题目
14.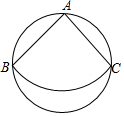 如图,从一块直径为24cm的圆形纸片上,剪出一个圆心角为90°的扇形ABC,使点A,B,C都在圆周上,将剪下的扇形围成一个圆锥的侧面,则这个圆锥的底面圆的半径是( )
如图,从一块直径为24cm的圆形纸片上,剪出一个圆心角为90°的扇形ABC,使点A,B,C都在圆周上,将剪下的扇形围成一个圆锥的侧面,则这个圆锥的底面圆的半径是( )
 如图,从一块直径为24cm的圆形纸片上,剪出一个圆心角为90°的扇形ABC,使点A,B,C都在圆周上,将剪下的扇形围成一个圆锥的侧面,则这个圆锥的底面圆的半径是( )
如图,从一块直径为24cm的圆形纸片上,剪出一个圆心角为90°的扇形ABC,使点A,B,C都在圆周上,将剪下的扇形围成一个圆锥的侧面,则这个圆锥的底面圆的半径是( )| A. | 3$\sqrt{2}$cm | B. | 2$\sqrt{3}$cm | C. | 6cm | D. | 12cm |
15.计算(27a8)÷($\frac{1}{3}{a}^{3}$)÷(9a2)的顺序不正确的是( )
| A. | (27a8)÷[($\frac{1}{3}{a}^{3}$)÷(9a2)] | B. | [(27a8)÷($\frac{1}{3}{a}^{3}$)]÷(9a2) | C. | (27$÷\frac{1}{3}÷9$)a8-3-2 | D. | [(27a3)÷(9a2)]÷($\frac{1}{3}{a}^{3}$) |
 如图,AB是⊙O的直径,⊙O与AC相交于点D,∠BAC=45°,AB=BC.
如图,AB是⊙O的直径,⊙O与AC相交于点D,∠BAC=45°,AB=BC.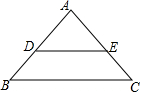 如图,在△ABC中,点D,E分别在AB,AC边上,且DE∥BC,若AD:DB=3:2,AE=6,则EC等于( )
如图,在△ABC中,点D,E分别在AB,AC边上,且DE∥BC,若AD:DB=3:2,AE=6,则EC等于( ) 如图,在?ABCD中,AC⊥BC,过点D作DE∥AC交BC的延长线于点E,连接AE交CD于点F.
如图,在?ABCD中,AC⊥BC,过点D作DE∥AC交BC的延长线于点E,连接AE交CD于点F.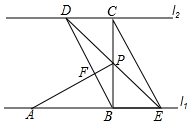 如图,直线l1∥l2,线段AB在l1上,BC⊥l1交l2于点C,且AB=BC=2cm,点P在点B、C之间,过点P的直线分别交l2、l1于点D、E;已知∠CDP=45°.
如图,直线l1∥l2,线段AB在l1上,BC⊥l1交l2于点C,且AB=BC=2cm,点P在点B、C之间,过点P的直线分别交l2、l1于点D、E;已知∠CDP=45°.