题目内容
破残的轮片上，弓形的弦AB长480mm，高CD为70mm，求原轮片的直径．
考点：垂径定理的应用,勾股定理
专题：
分析：由垂径定理，可得出BD的长；连接OB，在Rt△OBD中，可用半径OB表示出OD的长，进而可根据勾股定理求出得出轮子的半径，即可得出轮子的直径长．
解答：
解：连接OB；
Rt△OBD中，BD=
AB=240mm，
根据勾股定理得：
OD2+BD2=OB2，即：
（OB-70）2+2402=OB2，
解得：OB=
；
故轮子的直径为
mm．
解：连接OB；Rt△OBD中，BD=
| 1 |
| 2 |
根据勾股定理得：
OD2+BD2=OB2，即：
（OB-70）2+2402=OB2，
解得：OB=
| 3125 |
| 7 |
故轮子的直径为
| 6250 |
| 7 |
点评：此题主要考查了垂径定理及勾股定理的应用，准确作出辅助线构造直角三角形，进而利用勾股定理列出方程是解题的关键．
练习册系列答案
开心蛙口算题卡系列答案
相关题目
如图，已知直线AB、CD相交于点O，OB平分∠DOE，∠DOE=80°，则∠AOC=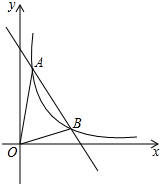
如图，一次函数y=-2x+8与反比例函数y=