题目内容
13. 南宁市在中国水城建设中,某施工队为引水需要欲拆除琶江岸边的一根电线杆AB(如图),已知距电线杆AB水平距离14米处是河岸,即BD=14米,该河岸的坡面CD的坡角∠CDF的正切值为2(即tan∠CDF=2),岸高CF为2米,在坡顶C处测得杆顶A的仰角为30°,D、E之间是宽2米的人行道.($\sqrt{3}$≈1.73).
南宁市在中国水城建设中,某施工队为引水需要欲拆除琶江岸边的一根电线杆AB(如图),已知距电线杆AB水平距离14米处是河岸,即BD=14米,该河岸的坡面CD的坡角∠CDF的正切值为2(即tan∠CDF=2),岸高CF为2米,在坡顶C处测得杆顶A的仰角为30°,D、E之间是宽2米的人行道.($\sqrt{3}$≈1.73).(1)求坡顶C离电线杆的距离CG;
(2)请你通过计算说明在拆除电线杆AB时,为确保安全,是否将此人行道封上?(在地面上以点B为圆心,以AB长为半径的圆形区域为危险区域)
分析 (1)在RT△CDF中,由tan∠CDF=2、CF=2,可求得DF,根据BF=GC=BD+DF可得;
(2)根据题意分析图形可得:在Rt△CDF中,由CF=2,tan∠CDF=2,可求得DE,进而得到BE的长.解Rt△AGC可得BE的值,通过比较BE、AB的大小即可求出答案.
解答 解:(1)由tan∠CDF=$\frac{CF}{DF}$=2,CF=2
∴DF=1,BG=2,
∵BD=14,
∴BF=GC=15,
答:坡顶C离电线杆的距离CG为15米;
(2)在Rt△AGC中,由tan30°=$\frac{\sqrt{3}}{3}$
∴AG=15×$\frac{\sqrt{3}}{3}$=5$\sqrt{3}$≈5×1.732=8.660米
∴AB=8.660+2=10.66米
BE=BD-ED=12米
∵BE>AB
∴不需要封人行道.
点评 本题考查俯角、仰角的定义,要求学生能借助俯角、仰角构造直角三角形并结合图形利用三角函数解直角三角形.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
15.化简$\frac{{x}^{2}-1}{x}÷\frac{x+1}{x}$的结果( )
| A. | x-1 | B. | x | C. | $\frac{1}{x}$ | D. | $\frac{1}{x-1}$ |
8.具备下列条件的三角形中,不能为直角三角形的是( )
| A. | ∠A+∠B=∠C | B. | ∠A=∠B=∠C/2 | C. | ∠A=90°-∠B | D. | ∠A-∠B=90° |
3.若一次函数y=kx+b的图象经过(-1,1),(0,m),(1,-5)三点,则m的值为( )
| A. | -1 | B. | -2 | C. | 0 | D. | $\frac{1}{2}$ |
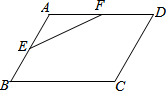 如图,在?ABCD中,E、F分别是AB、AD的中点,若△AEF的面积为5cm2,则?ABCD的面积是40cm2.
如图,在?ABCD中,E、F分别是AB、AD的中点,若△AEF的面积为5cm2,则?ABCD的面积是40cm2.