题目内容
3.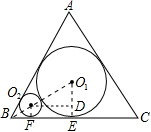 如图,在边长为54$\sqrt{3}$的正三角形ABC中,圆O1为△ABC的内切圆,圆O2与圆O1外切,且与AB、BC相切;圆O3与圆O2外切,且与AB、BC相切…如此继续下去,请计算圆O5的周长为$\frac{2}{3}$π.(结果保留π)
如图,在边长为54$\sqrt{3}$的正三角形ABC中,圆O1为△ABC的内切圆,圆O2与圆O1外切,且与AB、BC相切;圆O3与圆O2外切,且与AB、BC相切…如此继续下去,请计算圆O5的周长为$\frac{2}{3}$π.(结果保留π)
分析 本题可将三角形ABO分解成三个三角形,再根据三个三角形的面积之和等于△ABO的面积,即可得出半径的值,再根据题意依次列出⊙O2,⊙O3…的半径大小,找出规律即可.
解答  解:如图过点O2作O2D⊥O1E于D,
解:如图过点O2作O2D⊥O1E于D,
∵△ABC是等边三角形,O1为△ABC的内切圆,
∴O1E⊥BC,∠O1BE=∠O1O2D=30°,BE=$\frac{1}{2}$BC=27$\sqrt{3}$,
∴O1E=27,
设⊙O1,⊙O2的半径为R,r,
${{∴O}_{1}O}_{2}={\frac{1}{2}O}_{1}$D,
∴r=$\frac{1}{3}$R,
同理⊙O3的半径=$\frac{1}{3}$r=$\frac{1}{9}$R=3,
⊙O4=$\frac{1}{3}$×3=1,⊙O5=$\frac{1}{3}$×1=$\frac{1}{3}$,
∴⊙O5的周长=2×$\frac{1}{3}$π=$\frac{2}{3}$π.
点评 本题考查的是三角形的性质,解此类题目时要根据题意列出不等式,适当地对图形进行分解,然后再解题.

练习册系列答案
相关题目
18.已知三角形三边长分别为5cm、5cm、6cm,则这个三角形内切圆的半径是( )
| A. | $\frac{9}{8}$cm | B. | $\frac{3}{2}$cm | C. | 2cm | D. | 3cm |
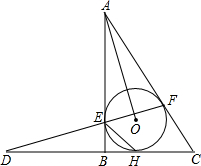 已知:如图,Rt△ABC外切于圆O,切点分别为E、F、H,∠ABC=90°,直线FE、CB交于D点,连接AO、HE.现给出以下四个结论:①∠FEH=90°-$\frac{1}{2}$∠C;②DE=AE;③AB2=AO•DF;④AE•CH=S△ABC,其中正确结论的序号为①③④.
已知:如图,Rt△ABC外切于圆O,切点分别为E、F、H,∠ABC=90°,直线FE、CB交于D点,连接AO、HE.现给出以下四个结论:①∠FEH=90°-$\frac{1}{2}$∠C;②DE=AE;③AB2=AO•DF;④AE•CH=S△ABC,其中正确结论的序号为①③④.