题目内容
15.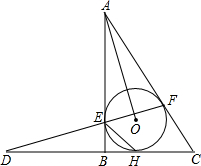 已知:如图,Rt△ABC外切于圆O,切点分别为E、F、H,∠ABC=90°,直线FE、CB交于D点,连接AO、HE.现给出以下四个结论:①∠FEH=90°-$\frac{1}{2}$∠C;②DE=AE;③AB2=AO•DF;④AE•CH=S△ABC,其中正确结论的序号为①③④.
已知:如图,Rt△ABC外切于圆O,切点分别为E、F、H,∠ABC=90°,直线FE、CB交于D点,连接AO、HE.现给出以下四个结论:①∠FEH=90°-$\frac{1}{2}$∠C;②DE=AE;③AB2=AO•DF;④AE•CH=S△ABC,其中正确结论的序号为①③④.
分析 连接OE,OH,OF,OB,
①由切线的性质和四边形的内角和即可得∠FOH=180°-∠C=90°+∠BAC,再根据圆周角定理即可得到结论正确;
②根据已知条件知道四边形OEBH是正方形,然后证明△BDE≌△FAO,然后利用全等三角形的对应边相等即可得出结论;
③根据已知条件可以证明△DFH∽△ABO,根据相似三角形的对应边成比例和已知条件即可证明结论正确;
④根据直角三角形的面积公式直接解答即可.
解答 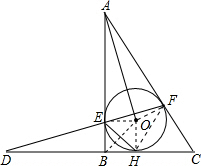 解:①连接OE,OH,OF,则OE⊥AB,OH⊥BC,
解:①连接OE,OH,OF,则OE⊥AB,OH⊥BC,
得出∠FOH=180°-∠C,
根据圆周角定理得∠FEH=$\frac{1}{2}$∠FOH=90$°-\frac{1}{2}$∠C;
故①正确;
②由①得四边形OEBH是正方形,
则圆的半径=BE,
∴OF=BE,
又∵∠DBE=∠AFO,∠BED=∠AEF=∠AFE,
在△BDE与△FAO中,
$\left\{\begin{array}{l}{∠DBE∠AFO}\\{OF=BE}\\{∠BED=∠AFE}\end{array}\right.$,
∴△BDE≌△FAO(SAS),
∴BD=AF,
∵BD<DE,
∴DE≠AF,
故②错误;
③∵Rt△ABC外切于⊙O,切点分别为E、F、H,
∴BE=BH,AF=AE,
根据②得BD=AF,
∴BD=AE(等量代换),
∴AB=DH;
连接OB、FH.
∵∠D=∠BAO,∠EFH=∠OBA=45°,
∴△DFH∽△ABO,
则DH•AB=AO•DF,又AB=DH,
所以AB2=AO•DF,
故③正确;
④设△ABC的三边分别为a,b,c,则AE=$\frac{b+c-a}{2}$,CH=$\frac{a+b-c}{2}$,AE•CH=$\frac{(b+c-a)}{2}$$•\frac{(a+b-c)}{2}$=$\frac{ab}{2}$=S△ABC.
故S△ABC=$\frac{1}{2}$AB•BC=AE•CH;
故④正确;
故答案为:①③④.
点评 本题考查了三角形的内切圆与内心.此题综合运用了切线的性质定理、切线长定理、圆周角定理和相似三角形的性质和判定,综合性比较强.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案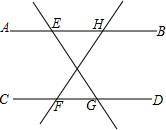 如图,下列条件中,不能判断直线AB∥CD的是( )
如图,下列条件中,不能判断直线AB∥CD的是( )| A. | ∠HEG=∠EGF | B. | ∠EHF+∠CFH=180° | C. | ∠EHF=∠CFH | D. | ∠AEG=∠DGE |
| A. | 5 | B. | -5 | C. | 0 | D. | 无法确定 |
| A. | 0.10 | B. | 0.12 | C. | 0.15 | D. | 0.18 |
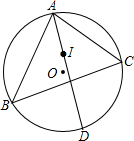 点I为△ABC的内心,AI的延长线交△ABC的外接圆于D,以D为圆心,DI为半径画弧,是否经过点B与点C?说明理由.
点I为△ABC的内心,AI的延长线交△ABC的外接圆于D,以D为圆心,DI为半径画弧,是否经过点B与点C?说明理由.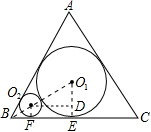 如图,在边长为54$\sqrt{3}$的正三角形ABC中,圆O1为△ABC的内切圆,圆O2与圆O1外切,且与AB、BC相切;圆O3与圆O2外切,且与AB、BC相切…如此继续下去,请计算圆O5的周长为$\frac{2}{3}$π.(结果保留π)
如图,在边长为54$\sqrt{3}$的正三角形ABC中,圆O1为△ABC的内切圆,圆O2与圆O1外切,且与AB、BC相切;圆O3与圆O2外切,且与AB、BC相切…如此继续下去,请计算圆O5的周长为$\frac{2}{3}$π.(结果保留π)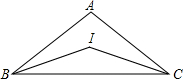 如图,△ABC中,AB=AC,∠ABC=40°,点I是△ABC的内心,则∠BAC的度数为100°.
如图,△ABC中,AB=AC,∠ABC=40°,点I是△ABC的内心,则∠BAC的度数为100°.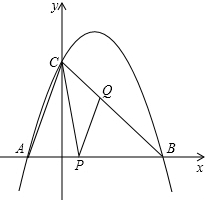 已知:二次函数y=ax2+bx+6(a≠0)的图象与x轴交于A、B两点(点A在点B的左侧),点A、点B的横坐标是方程x2-4x-12=0的两个根.
已知:二次函数y=ax2+bx+6(a≠0)的图象与x轴交于A、B两点(点A在点B的左侧),点A、点B的横坐标是方程x2-4x-12=0的两个根.