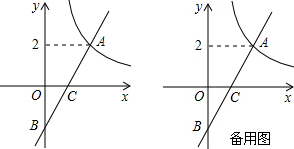题目内容
6. 如图,△ABC中,DE∥BC,DE=2,AD=3,DB=4,则BC的长是$\frac{14}{3}$.
如图,△ABC中,DE∥BC,DE=2,AD=3,DB=4,则BC的长是$\frac{14}{3}$.
分析 由平行可得对应线段成比例,即AD:AB=DE:BC,再把线段代入可求得BC.
解答 解:∵DE∥BC,
∴$\frac{AD}{AB}=\frac{DE}{BC}$,
∵AD=3,BD=4,
∴AB=7,
∴$\frac{3}{7}=\frac{2}{BC}$,
解得BC=$\frac{14}{3}$,
故答案为:$\frac{14}{3}$.
点评 本题主要考查平行线分线段成比例的性质,掌握平行线分线段成比例中的对应线段是解题的关键.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
5.下列计算正确的是( )
| A. | a•a3=a3 | B. | a4+a3=a2 | C. | (a2)5=a7 | D. | (-ab)2=a2b2 |
14.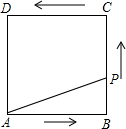 如图,正方形ABCD的边长为4,P为正方形边上一动点,运动路线是A→B→C→D→A,设P点经过的路程为x,以点A,P,B为顶点的三角形的面积是y,则下列图象能大致描述y与x的函数关系的是( )
如图,正方形ABCD的边长为4,P为正方形边上一动点,运动路线是A→B→C→D→A,设P点经过的路程为x,以点A,P,B为顶点的三角形的面积是y,则下列图象能大致描述y与x的函数关系的是( )
 如图,正方形ABCD的边长为4,P为正方形边上一动点,运动路线是A→B→C→D→A,设P点经过的路程为x,以点A,P,B为顶点的三角形的面积是y,则下列图象能大致描述y与x的函数关系的是( )
如图,正方形ABCD的边长为4,P为正方形边上一动点,运动路线是A→B→C→D→A,设P点经过的路程为x,以点A,P,B为顶点的三角形的面积是y,则下列图象能大致描述y与x的函数关系的是( )| A. | 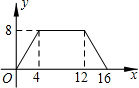 | B. | 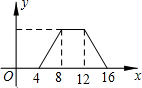 | C. | 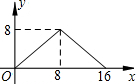 | D. | 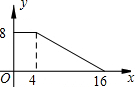 |
11.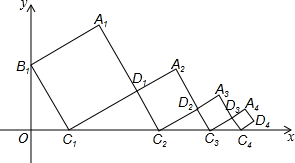 如图,平面直角坐标系中放置了四个正方形,其中相邻两个正方形的两边在同一直线上,已知正方形A1B1C1D1的边长为1,∠OC1B1=60°.若按此规律排列,第2015个小正方形最上面的顶点A2015的纵坐标是( )
如图,平面直角坐标系中放置了四个正方形,其中相邻两个正方形的两边在同一直线上,已知正方形A1B1C1D1的边长为1,∠OC1B1=60°.若按此规律排列,第2015个小正方形最上面的顶点A2015的纵坐标是( )
 如图,平面直角坐标系中放置了四个正方形,其中相邻两个正方形的两边在同一直线上,已知正方形A1B1C1D1的边长为1,∠OC1B1=60°.若按此规律排列,第2015个小正方形最上面的顶点A2015的纵坐标是( )
如图,平面直角坐标系中放置了四个正方形,其中相邻两个正方形的两边在同一直线上,已知正方形A1B1C1D1的边长为1,∠OC1B1=60°.若按此规律排列,第2015个小正方形最上面的顶点A2015的纵坐标是( )| A. | ($\frac{\sqrt{3}}{3}$)2014×($\frac{1+\sqrt{3}}{2}$) | B. | ($\frac{\sqrt{3}}{3}$)2015($\frac{1+\sqrt{3}}{2}$) | C. | ($\frac{\sqrt{3}}{2}$)2014×($\frac{1+\sqrt{3}}{3}$) | D. | ($\frac{\sqrt{3}}{2}$)2015×($\frac{1+\sqrt{3}}{3}$) |
16.已知直线y=kx+b,若k+b=-5,kb=5,那该直线不经过的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
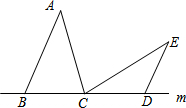 如图:在△ABC和△CDE中,AB=AC=CE,BC=DC=DE,AB>BC,∠BAC=∠DCE,点B,C,D在直线m上.以点C为旋转中心,将△CDE按逆时针方向旋转,使得CE与CA重合,得到△CD1E1(A).
如图:在△ABC和△CDE中,AB=AC=CE,BC=DC=DE,AB>BC,∠BAC=∠DCE,点B,C,D在直线m上.以点C为旋转中心,将△CDE按逆时针方向旋转,使得CE与CA重合,得到△CD1E1(A). 如图所示,过等边△ABC的顶点A,B,C依次作AB,BC,CA的垂线围成△A1B1C1,再过△A1B1C1的顶点A1、B1、C1依次作A1B1、B1C1、A1C1的垂线围成△A2B2C2…依照此规律直至构成△AnBnCn,若S△ABC=S,则S${\;}_{△{A}_{n}}$${\;}_{{B}_{n}}$${\;}_{{C}_{n}}$=3nS.
如图所示,过等边△ABC的顶点A,B,C依次作AB,BC,CA的垂线围成△A1B1C1,再过△A1B1C1的顶点A1、B1、C1依次作A1B1、B1C1、A1C1的垂线围成△A2B2C2…依照此规律直至构成△AnBnCn,若S△ABC=S,则S${\;}_{△{A}_{n}}$${\;}_{{B}_{n}}$${\;}_{{C}_{n}}$=3nS.