题目内容
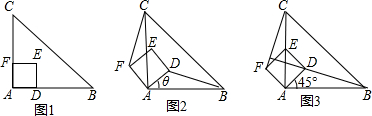
1. 如图所示,过等边△ABC的顶点A,B,C依次作AB,BC,CA的垂线围成△A1B1C1,再过△A1B1C1的顶点A1、B1、C1依次作A1B1、B1C1、A1C1的垂线围成△A2B2C2…依照此规律直至构成△AnBnCn,若S△ABC=S,则S${\;}_{△{A}_{n}}$${\;}_{{B}_{n}}$${\;}_{{C}_{n}}$=3nS.
如图所示,过等边△ABC的顶点A,B,C依次作AB,BC,CA的垂线围成△A1B1C1,再过△A1B1C1的顶点A1、B1、C1依次作A1B1、B1C1、A1C1的垂线围成△A2B2C2…依照此规律直至构成△AnBnCn,若S△ABC=S,则S${\;}_{△{A}_{n}}$${\;}_{{B}_{n}}$${\;}_{{C}_{n}}$=3nS.
分析 易证△ABC、△A1B1C1、△A2B2C2、…相似,设△ABC的边长为1,根据勾股定理求出A1B1=$\sqrt{3}$,A2B2=3,根据相似三角形面积比等于相似比的平方可知:S△A1B1C1=3S,S△A2B2C2=9S,S△A3B3C3=27S,于是S△AnBnC=3nS.
解答 解:设AB=1,在△A1AB1中
根据勾股定理A1A=$\frac{\sqrt{3}}{3}$,A1B=$\frac{2\sqrt{3}}{3}$,
∵A1A=BB1,
∴A1B1=$\sqrt{3}$,
∵△ABC、△A1B1C1、△A2B2C2、…相似,
∴$\frac{{S}_{△ABC}}{{S}_{△{A}_{1}{B}_{1}{C}_{1}}}$=($\frac{AB}{{A}_{1}{B}_{1}}$)2=$\frac{1}{3}$,
∵S△ABC=S,
∴S△A1B1C1=3S,
∴S△A2B2C2=9S,S△A3B3C3=27S,
依此类推,
S△AnBnCn=3nS.
故答案为:3nS.
点评 本题主要考查了三角形相似的判定与性质、勾股定理以及运用图形探索图形规律问题,发现相邻的两个三角形相似比为$\frac{1}{3}$是解决问题的关键.

练习册系列答案
相关题目
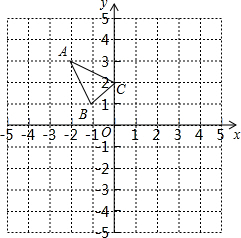 △ABC在平面直角坐标系xOy中的位置如所示.
△ABC在平面直角坐标系xOy中的位置如所示.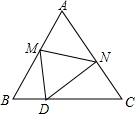 如图,在等边三角形纸片△ABC中,将纸片折叠,点A落在BC边上的点D处,MN为折痕,当DN⊥NC时,CN=1,则A、D两点之间的距离为$\sqrt{6}$.
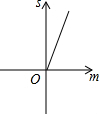
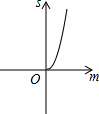
如图,在等边三角形纸片△ABC中,将纸片折叠,点A落在BC边上的点D处,MN为折痕,当DN⊥NC时,CN=1,则A、D两点之间的距离为$\sqrt{6}$.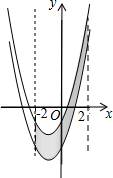 如图,已知抛物线y=x2+2x-3,把此抛物线沿y轴向上平移,平移后的抛物线和原抛物线与经过点(-2,0),(2,0)且平行于y轴的两条直线所围成的阴影部分的面积为s,平移的距离为m,则下列图象中,能表示s与m的函数关系的图象大致是( )
如图,已知抛物线y=x2+2x-3,把此抛物线沿y轴向上平移,平移后的抛物线和原抛物线与经过点(-2,0),(2,0)且平行于y轴的两条直线所围成的阴影部分的面积为s,平移的距离为m,则下列图象中,能表示s与m的函数关系的图象大致是( )

 如图,△ABC中,DE∥BC,DE=2,AD=3,DB=4,则BC的长是$\frac{14}{3}$.
如图,△ABC中,DE∥BC,DE=2,AD=3,DB=4,则BC的长是$\frac{14}{3}$.