题目内容
 如图,已知矩形OABC与矩形ODEF是位似图形,P是位似中心,若点B的坐标为(2,4),点E的坐标为(-1,2),则点P的坐标为( )
如图,已知矩形OABC与矩形ODEF是位似图形,P是位似中心,若点B的坐标为(2,4),点E的坐标为(-1,2),则点P的坐标为( )| A、(-4,0) |
| B、(-3,0) |
| C、(-2,0) |
| D、(-1.5,0) |
考点:位似变换,坐标与图形性质
专题:计算题
分析:根据位似变换的性质得
=
=
=
,则PO=OA=2,然后写出P点坐标.
| PO |
| PA |
| OD |
| AB |
| 2 |
| 4 |
| 1 |
| 2 |
解答:解:∵点B的坐标为(2,4),点E的坐标为(-1,2),
∴AB=4,OA=2,OD=2,
∵矩形OABC与矩形ODEF是位似图形,P是位似中心,
∴
=
=
=
,
∴PO=OA=2,
∴P点坐标为(-2,0).
故选C.
∴AB=4,OA=2,OD=2,
∵矩形OABC与矩形ODEF是位似图形,P是位似中心,
∴
| PO |
| PA |
| OD |
| AB |
| 2 |
| 4 |
| 1 |
| 2 |
∴PO=OA=2,
∴P点坐标为(-2,0).
故选C.
点评:本题考查了位似变换:如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形,这个点叫做位似中心.注意:两个图形必须是相似形;对应点的连线都经过同一点;对应边平行.

练习册系列答案
相关题目
已知x=2,y=-1是方程ax+y=3的一组解,则a的值( )
| A、1 | B、2 | C、-1 | D、-2 |
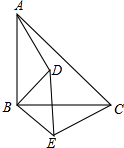 已知:如图,△ABC和△DBE均为等腰直角三角形.
已知:如图,△ABC和△DBE均为等腰直角三角形.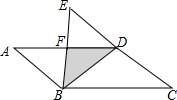 如图,已知四边形ABCD是一张平行四边形纸片,BD是一条对角线,且BD⊥DC,现沿BD将纸片翻折,使C点到达E点.
如图,已知四边形ABCD是一张平行四边形纸片,BD是一条对角线,且BD⊥DC,现沿BD将纸片翻折,使C点到达E点. 如图所示,AB∥CD,∠A=∠F,∠D=∠E,求∠EOF的度数.
如图所示,AB∥CD,∠A=∠F,∠D=∠E,求∠EOF的度数.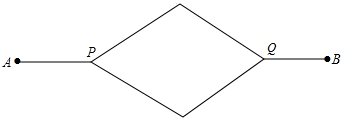 如图所示的道路,自A处出发通过P,Q到达B处,P,Q是三岔路口,假设当来到这些地点处就掷硬币,若出现正面就向右前进,若出现反面就向左前进,现若设掷硬币的次数是在四次以内,求到达B处的概率.
如图所示的道路,自A处出发通过P,Q到达B处,P,Q是三岔路口,假设当来到这些地点处就掷硬币,若出现正面就向右前进,若出现反面就向左前进,现若设掷硬币的次数是在四次以内,求到达B处的概率.