题目内容
如图1,把一张标准纸一次又一次对开,得到“2开”纸、“4开”纸、“8开”纸、“16开”纸、…,已知标准纸的短边长为a.(说明:①标准纸“2开”纸、“4开”纸、“8开”纸、“16开”纸、…都是矩形;②本题中所求边长或面积都用含a的代数式表示.)
(Ⅰ)如图2,把上面对开得到的“16开”纸按如下步骤折叠:
第一步:将矩形的短边AB与长边AD对齐折叠,点B落在AD上的点B′处,铺平后得折痕AE;
第二步:将长边AD与折痕AE对齐折叠,点D正好与点E重合,铺平后得折痕AF.则AD:AB的值是 ;
(Ⅱ)求“2开”纸长与宽的比 ;
(Ⅲ)如图3,由8个大小相等的小正方形构成“L”型图案,它的四个顶点E,F,G,H分别在“16开”纸的边AB,BC,CD,DA上,则DG的长 .

(Ⅰ)如图2,把上面对开得到的“16开”纸按如下步骤折叠:
第一步:将矩形的短边AB与长边AD对齐折叠,点B落在AD上的点B′处,铺平后得折痕AE;
第二步:将长边AD与折痕AE对齐折叠,点D正好与点E重合,铺平后得折痕AF.则AD:AB的值是
(Ⅱ)求“2开”纸长与宽的比
(Ⅲ)如图3,由8个大小相等的小正方形构成“L”型图案,它的四个顶点E,F,G,H分别在“16开”纸的边AB,BC,CD,DA上,则DG的长

考点:四边形综合题,全等三角形的判定与性质,勾股定理,矩形的性质,相似三角形的判定与性质
专题:操作型,探究型,几何变换
分析:(1)由折叠可得AD=AE,∠BAE=45°,根据勾股定理就能求出AD:AB的值.
(2)按照图1的折叠方法可得:“2开”纸的宽是“16开”纸的长的2倍“;“2开”纸的长是“16开”纸的宽的4倍,根据(1)中的结论即可解决问题.
(3)设DG的长为x,由于DC=
,则GC=
-x,易证△HDG~△GCF,△GCF≌△FBE,从而得到BF=CG=
-x,FC=2DG=2x,根据(1)中的结论可得BC=AD=
AB=
,根据BC=BE+EC即可建立关于x的方程,就可求出DG的长.
(2)按照图1的折叠方法可得:“2开”纸的宽是“16开”纸的长的2倍“;“2开”纸的长是“16开”纸的宽的4倍,根据(1)中的结论即可解决问题.
(3)设DG的长为x,由于DC=
| a |
| 4 |
| a |
| 4 |
| a |
| 4 |
| 2 |
| ||
| 4 |
解答:解:(1)如图2,由折叠可得:AD=AE,∠BAE=∠DAE=
∠BAD.
∵四边形ABCD是矩形,∴∠BAD=∠B=∠C=∠D=90°.
∴∠BAE=45°.∴∠BEA=45°.∴AB=BE.
∴AE2=AB2+BE2=2AB2.∴AE=
AB.
∴AD=AE=
AB.
∴AD:AB的值是
.
(2)如图1,由折叠可得:
“2开”纸的宽与“4开”纸的长相等,是“16开”纸的长的2倍;
“2开”纸的长是“8开”纸的长的2倍,是“16开”纸的宽4倍.
∵“2开”纸的长是a,∴“16开”纸的宽AB是
.
∵AD=
AB,∴“16开”纸的长AD是
.
∴“2开”纸的宽是
.
∴“2开”纸长与宽的比为a:
=
:1.
(3)∵四边形ABCD是矩形,∴DC=AB=
,BC=AD=
.
由图3可得:∠EFG=∠FGH=90°,EF=FG=2GH.
∵∠B=∠EFG=∠C=∠FGH∠D=90°,
∴∠BFE=90°-∠CFG=∠CGF,∠CGF=90°-∠DGH=∠DHG.
在△FCG和△GDH中,
∵∠C=∠D,∠CGF=∠DHG,
∴△FCG∽△GDH.
∴
=
.
∵FG=2GH,∴FC=2GD.
在△EBF和△FCG中,
∴△EBF≌△FCG.
∴BF=CG.
设DG=x,则BF=CG=DC-DG=
-x,FC═2GD=2x.
∵BC=BF+FC=
,∴
-x+2x=
.
∴x=
a.
∴DG的长为
a.
故答案为:
,
:1,
a.
| 1 |
| 2 |
∵四边形ABCD是矩形,∴∠BAD=∠B=∠C=∠D=90°.
∴∠BAE=45°.∴∠BEA=45°.∴AB=BE.
∴AE2=AB2+BE2=2AB2.∴AE=
| 2 |
∴AD=AE=
| 2 |
∴AD:AB的值是
| 2 |
(2)如图1,由折叠可得:
“2开”纸的宽与“4开”纸的长相等,是“16开”纸的长的2倍;
“2开”纸的长是“8开”纸的长的2倍,是“16开”纸的宽4倍.
∵“2开”纸的长是a,∴“16开”纸的宽AB是
| a |
| 4 |
∵AD=
| 2 |
| ||
| 4 |
∴“2开”纸的宽是
| ||
| 2 |
∴“2开”纸长与宽的比为a:
| ||
| 2 |
| 2 |
(3)∵四边形ABCD是矩形,∴DC=AB=
| a |
| 4 |
| ||
| 4 |
由图3可得:∠EFG=∠FGH=90°,EF=FG=2GH.
∵∠B=∠EFG=∠C=∠FGH∠D=90°,
∴∠BFE=90°-∠CFG=∠CGF,∠CGF=90°-∠DGH=∠DHG.
在△FCG和△GDH中,
∵∠C=∠D,∠CGF=∠DHG,
∴△FCG∽△GDH.
∴
| FC |
| GD |
| FG |
| GH |
∵FG=2GH,∴FC=2GD.
在△EBF和△FCG中,
|
∴△EBF≌△FCG.
∴BF=CG.
设DG=x,则BF=CG=DC-DG=
| a |
| 4 |
∵BC=BF+FC=
| ||
| 4 |
| a |
| 4 |
| ||
| 4 |
∴x=
| ||
| 4 |
∴DG的长为
| ||
| 4 |
故答案为:
| 2 |
| 2 |
| ||
| 4 |
点评:本题是操作探究类的一道试题,让学生在操作中探究,在探究中发现,考查了相似的性质与判定、全等的性质与判定、矩形的性质、勾股定理等知识,有一定的综合性,是一道体现新课程理念的好题.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
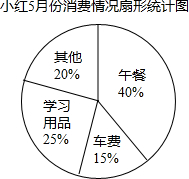 小红同学将自己5月份的各项消费情况制作成扇形统计图(如图),从图中可看出( )
小红同学将自己5月份的各项消费情况制作成扇形统计图(如图),从图中可看出( )| A、各项消费金额占消费总金额的百分比 |
| B、各项消费的金额 |
| C、消费的总金额 |
| D、各项消费金额的增减变化情况 |
 如图,把边长为a=2的正方形剪成四个全等的直角三角形,在下面对应的正方形网格(每个小正方形的边长均为1)中画出用这四个直角三角形按要求分别拼成的新的多边形(要求全部用上,互不重叠,互不留隙).
如图,把边长为a=2的正方形剪成四个全等的直角三角形,在下面对应的正方形网格(每个小正方形的边长均为1)中画出用这四个直角三角形按要求分别拼成的新的多边形(要求全部用上,互不重叠,互不留隙).
 如图,在Rt△ABC中,∠B=90°,分别以点A、C为圆心,大于
如图,在Rt△ABC中,∠B=90°,分别以点A、C为圆心,大于
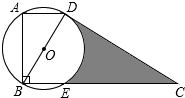 如图,在直角梯形ABCD中,∠ABC=90°,上底AD为
如图,在直角梯形ABCD中,∠ABC=90°,上底AD为 如图,在地面上的点A处测得树顶B的仰角为α度,AC=7米,则树高BC为
如图,在地面上的点A处测得树顶B的仰角为α度,AC=7米,则树高BC为