题目内容
 如图,在Rt△ABC中,∠B=90°,分别以点A、C为圆心,大于
如图,在Rt△ABC中,∠B=90°,分别以点A、C为圆心,大于| 1 |
| 2 |
(1)求∠ADE;(直接写出结果)
(2)当AB=3,AC=5时,求△ABE的周长.
考点:作图—基本作图,线段垂直平分线的性质,勾股定理的应用
专题:
分析:(1)根据题意可知MN是线段AC的垂直平分线,由此可得出结论;
(2)先根据勾股定理求出BC的长,再根据线段垂直平分线的性质即可得出结论.
(2)先根据勾股定理求出BC的长,再根据线段垂直平分线的性质即可得出结论.
解答:解:(1)∵由题意可知MN是线段AC的垂直平分线,
∴∠ADE=90°;
(2)∵在Rt△ABC中,∠B=90°,AB=3,AC=5,
∴BC=
=4,
∵MN是线段AC的垂直平分线,
∴AE=CE,
∴△ABE的周长=AB+(AE+BE)=AB+BC=3+4=7.
∴∠ADE=90°;
(2)∵在Rt△ABC中,∠B=90°,AB=3,AC=5,
∴BC=
| 52-32 |
∵MN是线段AC的垂直平分线,
∴AE=CE,
∴△ABE的周长=AB+(AE+BE)=AB+BC=3+4=7.
点评:本题考查的是作图-基本作图,熟知垂直平分线上任意一点,到线段两端点的距离相等是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

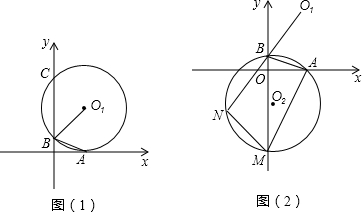
 经过点(1,1)的直线l:y=kx+2(k≠0)与反比例函数G1
经过点(1,1)的直线l:y=kx+2(k≠0)与反比例函数G1
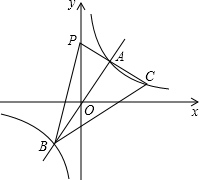 如图,在平面直角坐标系xOy中,直线y=
如图,在平面直角坐标系xOy中,直线y=