题目内容
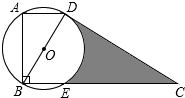 如图,在直角梯形ABCD中,∠ABC=90°,上底AD为
如图,在直角梯形ABCD中,∠ABC=90°,上底AD为| 3 |
考点:切线的性质,直角梯形,扇形面积的计算
专题:几何图形问题
分析:连接OE,根据∠ABC=90°,AD=
,∠ABD为30°,可得出AB与BD,可证明△OBE为等边三角形,即可得出∠C=30°.阴影部分的面积为直角梯形ABCD的面积-三角形ABD的面积-三角形OBE的面积-扇形ODE的面积.
| 3 |
解答:解:连接OE,过点O作OF⊥BE于点F.
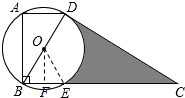
∵∠ABC=90°,AD=
,∠ABD为30°,
∴BD=2
,
∴AB=3,
∵OB=OE,∠DBC=60°,OF⊥BE,
∴OF=
,
∵CD为⊙O的切线,
∴∠BDC=90°,
∴∠C=30°,
∴BC=4
,
S阴影=S梯形ABCD-S△ABD-S△OBE-S扇形ODE
=
-
-
-
=
-
-
-π
=
-π.
故答案为:
-π.

∵∠ABC=90°,AD=
| 3 |
∴BD=2
| 3 |
∴AB=3,
∵OB=OE,∠DBC=60°,OF⊥BE,
∴OF=
| 3 |
| 2 |
∵CD为⊙O的切线,
∴∠BDC=90°,
∴∠C=30°,
∴BC=4
| 3 |
S阴影=S梯形ABCD-S△ABD-S△OBE-S扇形ODE
=
| (AD+BC)×AB |
| 2 |
| AD•AB |
| 2 |
| BE•OF |
| 2 |
120×π×(
| ||
| 360 |
=
(
| ||||
| 2 |
3
| ||
| 2 |
| ||||
| 2 |
=
21
| ||
| 4 |
故答案为:
21
| ||
| 4 |
点评:本题考查了切线的性质、直角梯形以及扇形面积的计算,要熟悉扇形的面积公式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
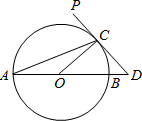 如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于点D,且∠D=2∠CAD.
如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于点D,且∠D=2∠CAD.
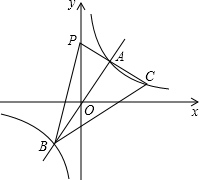 如图,在平面直角坐标系xOy中,直线y=
如图,在平面直角坐标系xOy中,直线y=