题目内容
3.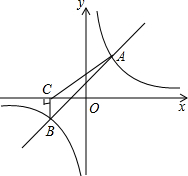 如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象相交于A、B两点,过点B作BC⊥x轴,垂足为C,已知A点的坐标是(2,3),BC=2.
如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象相交于A、B两点,过点B作BC⊥x轴,垂足为C,已知A点的坐标是(2,3),BC=2.(1)求反比例函数与一次函数的关系式;
(2)根据所给条件,请直接写出不等式kx+b-$\frac{m}{x}$>0的解集;
(3)求S△ABC.
分析 (1)由一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象相交于A(2,3)、B两点,首先求得反比例函数的解析式,则可求得B点的坐标,然后利用待定系数法即可求得一次函数的解析式;
(2)根据图象,观察即可求得答案;
(3)因为以BC为底,则BC边上的高为3+2=5,所以利用三角形面积的求解方法即可求得答案.
解答 解:(1)∵点A(2,3)在反比例函数y=$\frac{m}{x}$的图象上,
∴m=2×3=6,
∴反比例函数的解析式为:y=$\frac{6}{x}$,
∵BC=2.
∴B的纵坐标为-2,
代入得,-2=$\frac{6}{x}$,
解得x=-3,
∴B(-3,-2),
∵A(2,3),B(-3,-2)两点在y=kx+b上,
∴$\left\{\begin{array}{l}{2k+b=3}\\{-3k+b=-2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=1}\\{b=1}\end{array}\right.$,
∴一次函数的解析式为:y=x+1;
(2)不等式kx+b-$\frac{m}{x}$>0的解集为:-3<x<0或x>2;
(3)以BC为底,则BC边上的高为3+2=5,
∴S△ABC=$\frac{1}{2}$×2×5=5.
点评 此题考查了反比例函数与一次函数的交点问题.注意待定系数法的应用是解题的关键.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
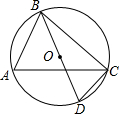 如图,⊙O的直径BD=4,∠A=60°,则CD的长度为2.
如图,⊙O的直径BD=4,∠A=60°,则CD的长度为2.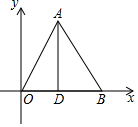 如图,△AOB是等边三角形,B点的坐标为(6,0),AD是高.
如图,△AOB是等边三角形,B点的坐标为(6,0),AD是高.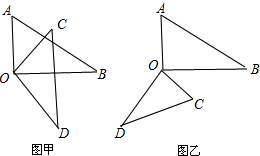 如图甲,将一副三角板的两个直角顶点重合在一起放置.
如图甲,将一副三角板的两个直角顶点重合在一起放置.