题目内容
12.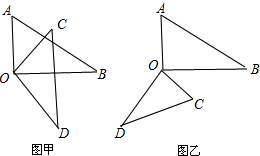 如图甲,将一副三角板的两个直角顶点重合在一起放置.
如图甲,将一副三角板的两个直角顶点重合在一起放置.(1)当∠BOC=60°时,∠AOD=120°.
当∠BOC=70°时,∠AOD=110°.
(2)如图乙,∠AOC与∠BOD的大小关系如何?请说明理由.
(3)若把三角板COD绕点O顺时针旋转到如图②的位置时,(2)中的结论还成立吗?为什么?
分析 (1)∠AOC+∠BOC=90°,∠COD=90°,于是∠AOD+∠BOC=∠AOC+∠COD+∠BOC=∠AOC+∠BOC+∠COD,然后把∠AOC+∠BOC=90°,∠COD=90°代入计算即可.
(2)由互余两角的关系即可得出结论;
(3)由角的关系即可得出结论.
解答 解:(1)根据题意得∠AOC+∠BOC=90°,∠COD=90°,
∴∠AOD+∠BOC=∠AOC+∠COD+∠BOC=∠AOC+∠BOC+∠COD=90°+90°=180°.
当∠BOC=60°时,∠AOD=120°;
当∠BOC=70°时,∠AOD=110°;
故答案为120°,110°;
(2)∠AOC=∠BOD,理由如下:
∵∠AOC+∠BOC=90°,∠BOD+∠BOC=90°,
∴∠AOC=∠BOD;
(3)成立,∠AOC=∠BOD;理由如下:
∵∠AOC=∠AOB+∠BOC=90°+∠BOC,
∠BOD=∠COD+∠BOC=90°+∠BOC,
∴∠AOC=∠BOD.
点评 本题考查了余角和补角、角的计算;熟练掌握角之间的关系是解决问题的关键.

练习册系列答案
相关题目
4.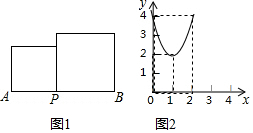 如图1,AB=2,P是线段AB上一点,分别以AP、BP为边作正方形,设AP=x,这两个正方形的面积之和为S,且S与x之间的关系如图2所示,则下列说法中正确的是( )
如图1,AB=2,P是线段AB上一点,分别以AP、BP为边作正方形,设AP=x,这两个正方形的面积之和为S,且S与x之间的关系如图2所示,则下列说法中正确的是( )
 如图1,AB=2,P是线段AB上一点,分别以AP、BP为边作正方形,设AP=x,这两个正方形的面积之和为S,且S与x之间的关系如图2所示,则下列说法中正确的是( )
如图1,AB=2,P是线段AB上一点,分别以AP、BP为边作正方形,设AP=x,这两个正方形的面积之和为S,且S与x之间的关系如图2所示,则下列说法中正确的是( )| A. | 在点P由点A向点B运动过程中,S有最小值为2 | |
| B. | 在点P由点A向点B运动过程中,S的值不变 | |
| C. | S与x之间的关系式为S=2x2-4 | |
| D. | 当0<x<1时,S的值越来越大 |
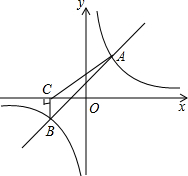 如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象相交于A、B两点,过点B作BC⊥x轴,垂足为C,已知A点的坐标是(2,3),BC=2.
如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象相交于A、B两点,过点B作BC⊥x轴,垂足为C,已知A点的坐标是(2,3),BC=2. 如图是一个汉字“互”字,其中,AB∥CD,∠1=∠2,∠MGH=∠MEF.求证:∠MEF=∠GHN.
如图是一个汉字“互”字,其中,AB∥CD,∠1=∠2,∠MGH=∠MEF.求证:∠MEF=∠GHN.