题目内容
4. 如图,AB是圆O的直径,弦CD⊥AB于点E,点P在圆O上且∠1=∠C.
如图,AB是圆O的直径,弦CD⊥AB于点E,点P在圆O上且∠1=∠C.(1)求证:CB∥PD;
(2)若BC=3,BE=2,求CD的长.
分析 (1)要证明CB∥PD,只要证明∠1=∠P;由∠1=∠C,∠P=∠C,可得∠1=∠P,即可解决问题.
(2)首先运用勾股定理求出CE的长度,然后运用垂径定理证明CE=DE,即可解决问题.
解答  (1)证明:如图,∵∠1=∠C,∠P=∠C,
(1)证明:如图,∵∠1=∠C,∠P=∠C,
∴∠1=∠P,
∴CB∥PD.
(2)解:∵CE⊥BE,
∴CE2=CB2-BE2,而CB=3,BE=2,
∴CE=$\sqrt{5}$;而AB⊥CD,
∴DE=CE,CD=2CE=2$\sqrt{5}$.
点评 主要考查了圆周角定理、垂径定理、勾股定理等几何知识点及其应用问题;牢固掌握圆周角定理、垂径定理、勾股定理等几何知识点是基础,灵活运用、解答是关键.

练习册系列答案
相关题目
14.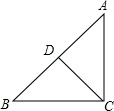 如图,在△ABC中,点D在AB上,下列条件能使△BCD和△ABC相似的是( )
如图,在△ABC中,点D在AB上,下列条件能使△BCD和△ABC相似的是( )
 如图,在△ABC中,点D在AB上,下列条件能使△BCD和△ABC相似的是( )
如图,在△ABC中,点D在AB上,下列条件能使△BCD和△ABC相似的是( )| A. | ∠ACD=∠B | B. | ∠ADC=∠ACB | C. | AC2=AD•AB | D. | BC2=BD•BA |
19.已知反比例函数图象经过点(1,-1),(m,1),则m等于( )
| A. | 2 | B. | -2 | C. | 1 | D. | -1 |
13.节能电动车越来越受到人们的喜爱,新开发的各种品牌电动车相继投放市场,涛伟车行经营的A型节能电动车去年销售总额为m万元,今年每辆A型节能电动车的销售价比去年降低2000元.若今年和去年卖出的节能电动车的数量相同(同一型号的节能电动车每辆的销售价格相同),则今年的销售总额将比去年减少20%.
(1)今年A型节能电动车每辆售价多少万元?(用列方程的方法解答)
(2)涛伟车行清明节后计划新购进一批A型节能电动车和新款B型节能电动车,进货时,每购进3辆节能电动车,批发商就给车行返回1500元.若新款B型节能电动车的进货数量是A型节能电动车的进货数量的2倍,全部销售获得的利润不少于18万元,且今年A,B两种型号节能电动车的进货和销售价格如下表:
那么新款B型节能电动车至少要购进多少辆?
(1)今年A型节能电动车每辆售价多少万元?(用列方程的方法解答)
(2)涛伟车行清明节后计划新购进一批A型节能电动车和新款B型节能电动车,进货时,每购进3辆节能电动车,批发商就给车行返回1500元.若新款B型节能电动车的进货数量是A型节能电动车的进货数量的2倍,全部销售获得的利润不少于18万元,且今年A,B两种型号节能电动车的进货和销售价格如下表:
| A型节能电动车 | B型节能电动车 | |
| 进货价格(万元/辆) | 0.55 | 0.7 |
| 销售价格(万元/辆) | 今年的销售价格 | 2 |
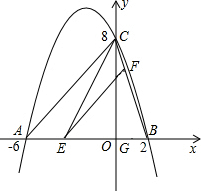 已知:抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,线段OB、OC的长(OB<OC)是方程x2-10x+16=0的两个根,且抛物线的对称轴是直线x=-2.
已知:抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,线段OB、OC的长(OB<OC)是方程x2-10x+16=0的两个根,且抛物线的对称轴是直线x=-2.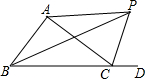 如图,△ABC的外角∠ACD的平分线CP与内角∠ABC的平分线BP交于点P,连接AP,CP,若∠APC=65°,则∠ABC=50°.
如图,△ABC的外角∠ACD的平分线CP与内角∠ABC的平分线BP交于点P,连接AP,CP,若∠APC=65°,则∠ABC=50°. 如图,把一段铁丝分成相等的三段,则可围成边长为($\frac{1}{3}$a2+$\frac{13}{3}$)(cm)的等边三角形,若把这一段铁丝分成相等的四段,则可围成边长为($\frac{3}{2}$a+1)(cm)的正方形,求该段铁丝的长.
如图,把一段铁丝分成相等的三段,则可围成边长为($\frac{1}{3}$a2+$\frac{13}{3}$)(cm)的等边三角形,若把这一段铁丝分成相等的四段,则可围成边长为($\frac{3}{2}$a+1)(cm)的正方形,求该段铁丝的长.