题目内容
13.节能电动车越来越受到人们的喜爱,新开发的各种品牌电动车相继投放市场,涛伟车行经营的A型节能电动车去年销售总额为m万元,今年每辆A型节能电动车的销售价比去年降低2000元.若今年和去年卖出的节能电动车的数量相同(同一型号的节能电动车每辆的销售价格相同),则今年的销售总额将比去年减少20%.(1)今年A型节能电动车每辆售价多少万元?(用列方程的方法解答)
(2)涛伟车行清明节后计划新购进一批A型节能电动车和新款B型节能电动车,进货时,每购进3辆节能电动车,批发商就给车行返回1500元.若新款B型节能电动车的进货数量是A型节能电动车的进货数量的2倍,全部销售获得的利润不少于18万元,且今年A,B两种型号节能电动车的进货和销售价格如下表:
| A型节能电动车 | B型节能电动车 | |
| 进货价格(万元/辆) | 0.55 | 0.7 |
| 销售价格(万元/辆) | 今年的销售价格 | 2 |
分析 (1)设今年A型节能电动车每辆售价x万元,则去年售价每辆为(x+0.2)万元,由卖出的数量相同建立方程求出其解即可;
(2)设今年新进B型节能电动车a辆,则A型节能电动车$\frac{a}{2}$辆,获利y元,由条件表示出y与a之间的关系式,由a的取值范围就可以求出y的最大值.
解答 解:(1)设今年A型车每辆售价x万元,则去年售价每辆为(x+0.2)万元,由题意,得
$\frac{m}{x+0.2}$=$\frac{m(1-20%)}{x}$,
解得:x=0.8.
经检验,x=0.8是原方程的根.
答:今年A型车每辆售价0.8万元;
(2)设今年新进B型节能电动车a辆,则A型节能电动车$\frac{a}{2}$辆,获利y元,依题意得
y=a(20000-0.7×10000)+$\frac{a}{2}$(8000-0.55×10000)+1500×$\frac{a+\frac{a}{2}}{3}$≥180000,
解得 a≥12.
因为a是整数,所以a=12.
答:新款B型节能电动车至少要购进12辆.
点评 本题考查了列分式方程解实际问题的运用,分式方程的解法的运用,一次函数的解析式的运用,解答时由销售问题的数量关系求出一次函数的解析式是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
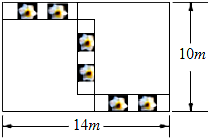 某市举办花展,如图,在长为14m,宽为10m的长方形展厅,划出三个形状、大小完全一样的小长方形摆放水仙花,则每个小长方形的周长为( )
某市举办花展,如图,在长为14m,宽为10m的长方形展厅,划出三个形状、大小完全一样的小长方形摆放水仙花,则每个小长方形的周长为( ) 如图,AB是圆O的直径,弦CD⊥AB于点E,点P在圆O上且∠1=∠C.
如图,AB是圆O的直径,弦CD⊥AB于点E,点P在圆O上且∠1=∠C.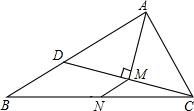 如图,在△ABC中,AB=5,AC=3,点N为BC的中点,AM平分∠BAC,CM⊥AM,垂足为点M,延长CM交AB于点D,求MN的长.
如图,在△ABC中,AB=5,AC=3,点N为BC的中点,AM平分∠BAC,CM⊥AM,垂足为点M,延长CM交AB于点D,求MN的长.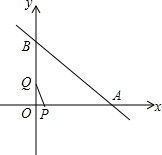 如图,直线y=-x+8与x轴、y轴交于A、B两点,点P、点Q同时从点O出发,分别以每秒3个单位和每秒4个单位的速度沿x轴、y轴方向移动,连接PQ.设移动的时间为t秒(0<t<2),以点P为中心,顺时针旋转△POQ,使旋转后的△O′PQ′的边PQ′恰好落在x轴上.
如图,直线y=-x+8与x轴、y轴交于A、B两点,点P、点Q同时从点O出发,分别以每秒3个单位和每秒4个单位的速度沿x轴、y轴方向移动,连接PQ.设移动的时间为t秒(0<t<2),以点P为中心,顺时针旋转△POQ,使旋转后的△O′PQ′的边PQ′恰好落在x轴上.