题目内容
9.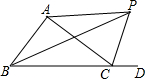 如图,△ABC的外角∠ACD的平分线CP与内角∠ABC的平分线BP交于点P,连接AP,CP,若∠APC=65°,则∠ABC=50°.
如图,△ABC的外角∠ACD的平分线CP与内角∠ABC的平分线BP交于点P,连接AP,CP,若∠APC=65°,则∠ABC=50°.
分析 延长BA,作PN⊥BD于N,PF⊥BA于F,PM⊥AC于M,如图,根据角平分线定理得到PN=PF,PN=PM,则PM=PF,再根据角平分线定理的逆定理得到AP平分∠CAF,即∠PAC=∠PAF,在△PAC中,利用三角形内角和定理得∠PAC+∠PCA=115°,则∠FAC+∠ACD=2(∠PAC+∠PCA)=230°,接着利用三角形外角性质得∠FAC=∠ABC+∠ACB,所以∠ABC+∠ACB+∠ACD=230°,易得∠ABC=50°.
解答 解:延长BA,作PN⊥BD于N,PF⊥BA于F,PM⊥AC于M,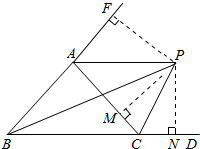 如图,
如图,
∵PB平分∠ABC,
∴PN=PF,
∵PC平分∠ACD,
∴PN=PM,∠PCA=∠PCD,
∴PM=PF,
∴AP平分∠CAF,
∴∠PAC=∠PAF,
在△PAC中,∵∠PAC+∠PCA+∠APC=180°,
∴∠PAC+∠PCA=180°-65°=115°,
∴∠FAC+∠ACD=2(∠PAC+∠PCA)=230°,
∵∠FAC=∠ABC+∠ACB,
∴∠ABC+∠ACB+∠ACD=230°,
而∠ACB+∠ACD=180°,
∴∠ABC=230°-180°=50°.
故答案为50°.
点评 本题考查了三角形内角和定理:三角形内角和是180°.也考查了角平分线定理和逆定理.证明PA为∠BAC的外角平分线是解题的关键.

练习册系列答案
相关题目
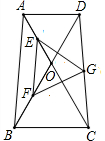 在梯形ABCD中,AD∥BC,AB=CD,∠AOD=60°,E为OA的中点,F为OB的中点,G为CD的中点,试判断△EFG的形状并说明理由.
在梯形ABCD中,AD∥BC,AB=CD,∠AOD=60°,E为OA的中点,F为OB的中点,G为CD的中点,试判断△EFG的形状并说明理由. 如图,AB是圆O的直径,弦CD⊥AB于点E,点P在圆O上且∠1=∠C.
如图,AB是圆O的直径,弦CD⊥AB于点E,点P在圆O上且∠1=∠C. 小李家用40m长的篱笆围成一个一边靠墙(墙足够长)的矩形菜园,如图.
小李家用40m长的篱笆围成一个一边靠墙(墙足够长)的矩形菜园,如图.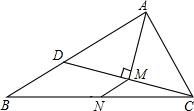 如图,在△ABC中,AB=5,AC=3,点N为BC的中点,AM平分∠BAC,CM⊥AM,垂足为点M,延长CM交AB于点D,求MN的长.
如图,在△ABC中,AB=5,AC=3,点N为BC的中点,AM平分∠BAC,CM⊥AM,垂足为点M,延长CM交AB于点D,求MN的长.