题目内容
9. 某地需要开辟一条隧道,隧道AB的长度无法直接测量.如图所示,在地面上取一点C,使C到A、B两点均可直接到达,测量找到AC和BC的中点D、E,测得DE的长为1100m,则隧道AB的长度为( )
某地需要开辟一条隧道,隧道AB的长度无法直接测量.如图所示,在地面上取一点C,使C到A、B两点均可直接到达,测量找到AC和BC的中点D、E,测得DE的长为1100m,则隧道AB的长度为( )| A. | 3300 m | B. | 2200 m | C. | 1100 m | D. | 550 m |
分析 由D为AC的中点、E为BC的中点,可得出DE为△ABC的中位线,根据DE的长度结合三角形中位线定理即可得出AB的长度.
解答 解:∵D为AC的中点,E为BC的中点,
∵DE为△ABC的中位线,
又∵DE=1100m,
∴AB=2DE=2200m.
故选B.
点评 本题考查了三角形中位线定理,根据DE的长度结合三角形中位线定理求出AB的长是解题的关键.

练习册系列答案
相关题目
17.若一次函数y=kx+b的图象经过第二、三、四象限,则k、b的取值范围是( )
| A. | k>0,b>0 | B. | k>0,b<0 | C. | k<0,b<0 | D. | k<0,b>0 |
4.关于y=2(x-3)2+2的图象,下列叙述正确的是( )
| A. | 顶点坐标为(-3,2) | B. | 对称轴为直线y=3 | ||
| C. | 当x>3时,y随x增大而增大 | D. | 与y轴交于点(0,2) |
14.如果x=0是关于x的方程3x-2a=4的解,则a的值是( )
| A. | 2 | B. | -2 | C. | $\frac{4}{3}$ | D. | -$\frac{4}{3}$ |
18. 如图所示,实数a、b在数轴上的位置,化简:$\sqrt{(a-b)^{2}}$-$\sqrt{{a}^{2}}$-$\sqrt{(b-1)^{2}}$=( )
如图所示,实数a、b在数轴上的位置,化简:$\sqrt{(a-b)^{2}}$-$\sqrt{{a}^{2}}$-$\sqrt{(b-1)^{2}}$=( )
 如图所示,实数a、b在数轴上的位置,化简:$\sqrt{(a-b)^{2}}$-$\sqrt{{a}^{2}}$-$\sqrt{(b-1)^{2}}$=( )
如图所示,实数a、b在数轴上的位置,化简:$\sqrt{(a-b)^{2}}$-$\sqrt{{a}^{2}}$-$\sqrt{(b-1)^{2}}$=( )| A. | 2b-2a-1 | B. | -2a+1 | C. | 1 | D. | 2b-1 |
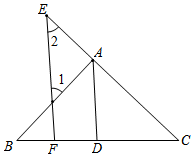 完成以下推理,并在括号中写出相应的根据
完成以下推理,并在括号中写出相应的根据 如图,在平面直角坐标系中,已知点A(0,3),且△OAB≌△O'A'B',点A的对应点A'在直线y=$\frac{3}{4}$x上,A'O'⊥x轴于O'点,则点B与其对应点B'间的距离为4.
如图,在平面直角坐标系中,已知点A(0,3),且△OAB≌△O'A'B',点A的对应点A'在直线y=$\frac{3}{4}$x上,A'O'⊥x轴于O'点,则点B与其对应点B'间的距离为4.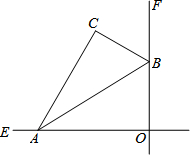 如图,直线OE与直线OF互相垂直,将含30°的三角尺ABC如图摆放,其斜边两端点A、B分别落在OE、OF上,且AB=12cm
如图,直线OE与直线OF互相垂直,将含30°的三角尺ABC如图摆放,其斜边两端点A、B分别落在OE、OF上,且AB=12cm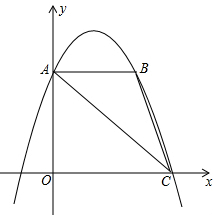 如图,已知抛物线y=-x2+bx+c经过点A(0,3),C(3,0);过A作AB∥x轴交抛物线于点B,连接AC、BC,点P为抛物线上动点.
如图,已知抛物线y=-x2+bx+c经过点A(0,3),C(3,0);过A作AB∥x轴交抛物线于点B,连接AC、BC,点P为抛物线上动点.