题目内容
18．
如图所示，实数a、b在数轴上的位置，化简：$\sqrt{（a-b）^{2}}$-$\sqrt{{a}^{2}}$-$\sqrt{（b-1）^{2}}$=（ ）| A． | 2b-2a-1 | B． | -2a+1 | C． | 1 | D． | 2b-1 |
分析 直接利用数轴得出a-b＜0，a＜0，b-1＞0，进而化简求出答案．
解答 解：由数轴可得：a-b＜0，a＜0，b-1＞0，
故$\sqrt{（a-b）^{2}}$-$\sqrt{{a}^{2}}$-$\sqrt{（b-1）^{2}}$=b-a+a-（b-1）
=1．
故选：C．
点评 此题主要考查了二次根式的性质与化简，正确得出各项符号是解题关键．
练习册系列答案
相关题目
9．
某地需要开辟一条隧道，隧道AB的长度无法直接测量．如图所示，在地面上取一点C，使C到A、B两点均可直接到达，测量找到AC和BC的中点D、E，测得DE的长为1100m，则隧道AB的长度为（ ）
某地需要开辟一条隧道，隧道AB的长度无法直接测量．如图所示，在地面上取一点C，使C到A、B两点均可直接到达，测量找到AC和BC的中点D、E，测得DE的长为1100m，则隧道AB的长度为（ ）| A． | 3300 m | B． | 2200 m | C． | 1100 m | D． | 550 m |
6．购买单价为a元的练习本2本和b支单价是3元的圆珠笔，则总价是（ ）元．
| A． | a+b | B． | 2a+b | C． | 2a+3b | D． | a+3b |
13．四位同学画数轴如下图所示，你认为正确的是（ ）
| A． |  | B． |  | ||
| C． |  | D． |  |
3．关于x的不等式组$\left\{\begin{array}{l}x＞a\\ x＞2-a\end{array}\right.$的解集是x＞a，则a的取值范围是（ ）
| A． | a＞1 | B． | a≤1 | C． | a≥1 | D． | a＜1 |
10．方程4x-1=3的解是（ ）
| A． | x=1 | B． | x=-1 | C． | x=2 | D． | x=-2 |
7．下列合并同类项中正确的是（ ）
| A． | 5xy-xy=5 | B． | m+m=m2 | C． | -y-y=0 | D． | -2xy+2xy=0 |
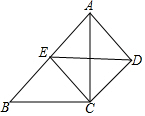如图，CD∥AB，且CD=$\frac{1}{2}$AB，点E为AB的中点，若四边形ADCE为正方形，则∠B=45°．