题目内容
1.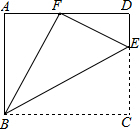 如图,点E是矩形ABCD中CD边上一点,△BCE沿BE折叠为△BFE,点F落在AD上.
如图,点E是矩形ABCD中CD边上一点,△BCE沿BE折叠为△BFE,点F落在AD上.(1)求证:△ABF∽△DFE;
(2)若sin∠DFE=$\frac{1}{3}$,求tan∠EBC的值.
(3)设$\frac{AB}{BC}$=k,是否存在k的值,使△ABF与△BFE相似?,若存在,求出k的值;若不存在,请说明理由.
分析 (1)根据矩形的性质可知∠A=∠D=∠C=90°,△BCE沿BE折叠为△BFE,得出∠BFE=∠C=90°,再根据三角形的内角和为180°,可知∠AFB+∠ABF=90°,得出∠ABF=∠DFE,即可证明△ABF∽△DFE;
(2)已知sin∠DFE=$\frac{1}{3}$,设DE=a,EF=3a,DF=2$\sqrt{2}$a,可得出CE=EF=3a,CD=DE+CE=4a,AB=4a,∠EBC=∠EBF,由(1)中△ABF∽△DFE,可得tan∠EBC=tan∠EBF=$\frac{\sqrt{2}}{2}$;
(3)分类讨论:①△ABF∽△FBE;②△ABF∽△FEB时求出k的值.
解答 (1)证明:∵四边形ABCD是矩形
∴∠A=∠D=∠C=90°,
∵△BCE沿BE折叠为△BFE,
∴∠BFE=∠C=90°,
∴∠AFB+∠DFE=180°-∠BFE=90°,
又∵∠AFB+∠ABF=90°,
∴∠ABF=∠DFE,
∴△ABF∽△DFE;
(2)解:在Rt△DEF中,sin∠DFE=$\frac{DE}{EF}$=$\frac{1}{3}$,
∴设DE=a,EF=3a,DF=$\sqrt{E{F}^{2}D{E}^{2}}$=2$\sqrt{2}$a,
∵△BCE沿BE折叠为△BFE,
∴CE=EF=3a,CD=DE+CE=4a,AB=4a,∠EBC=∠EBF,
又∵△ABF∽△DFE,
∴$\frac{EF}{BF}$=$\frac{DF}{AB}$=$\frac{2\sqrt{2}a}{4a}$=$\frac{\sqrt{2}}{2}$,
∴tan∠EBF=$\frac{EF}{BF}$=$\frac{\sqrt{2}}{2}$,
tan∠EBC=tan∠EBF=$\frac{\sqrt{2}}{2}$;
(3)当△ABF∽△FBE时,∠2=∠4.
∵∠4=∠5,∠2+∠4+∠5=90°,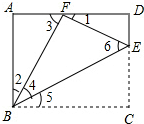
∴∠2=∠4=∠5=30°,
∴$\frac{AB}{BF}$=cos30°=$\frac{\sqrt{3}}{2}$,
∵BC=BF,
∴$\frac{AB}{BC}$=k=$\frac{\sqrt{3}}{2}$;
②当△ABF∽△FEB时,∠2=∠6,
∵∠4+∠6=90°,
∴∠2+∠4=90°,
这与∠2+∠4+∠5=90°相矛盾,
∴△ABF∽△FEB不成立.
综上所述,k=$\frac{\sqrt{3}}{2}$时,△ABF与△BFE相似.
点评 本题考查的是矩形的性质、相似三角形的判定和性质以及锐角三角函数的概念,掌握有两个角相等的两个三角形相似是解题的关键,注意分情况讨论思想的灵活运用.

| A. | 扇形统计图 | B. | 折线统计图 | C. | 条形统计图 | D. | 以上都可以 |
| A. | a+3a=4a2 | B. | a4•a4=2a4 | C. | (a2)3=a5 | D. | (-a)3÷(-a)=a2 |

| A. | ① | B. | ①② | C. | ①②③ | D. | ①③④ |
| A. | 也扩大2倍 | B. | 缩小为原来的$\frac{1}{2}$ | C. | 都不变 | D. | 不能确定 |
| A. | 29 | B. | -17 | C. | 7 | D. | 5 |
 将一副三角板(△BAC和△ADE)如图放置,若AE∥BC,则∠CAE=30度,∠AFD=75度.
将一副三角板(△BAC和△ADE)如图放置,若AE∥BC,则∠CAE=30度,∠AFD=75度.