题目内容
10.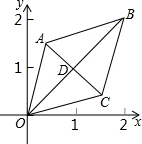 如图,已知菱形OABC的两个顶点O(0,0),B(2,2),若将菱形绕点O以每秒45°的速度逆时针旋转,则第2017秒时,菱形两对角线交点D的纵坐标为( )
如图,已知菱形OABC的两个顶点O(0,0),B(2,2),若将菱形绕点O以每秒45°的速度逆时针旋转,则第2017秒时,菱形两对角线交点D的纵坐标为( )| A. | -1 | B. | 1 | C. | -$\sqrt{2}$ | D. | $\sqrt{2}$ |
分析 根据菱形的性质及中点的坐标公式可得点D坐标,再根据旋转的性质可得旋转后点D的坐标,进而可求出其纵坐标.
解答 解:菱形OABC的顶点O(0,0),B(2,2),得
D点坐标为($\frac{0+2}{2}$,$\frac{0+2}{2}$),即(1,1).
每秒旋转45°,则第2017秒时,得45°×2017,
45°×2017÷360=252.125周,
∵OD旋转了252周半,
∴菱形的对角线交点D的坐标为(0,$\sqrt{2}$),
∴菱形两对角线交点D的纵坐标为$\sqrt{2}$,
故选D.
点评 本题主要考查菱形的性质及旋转的性质,熟练掌握菱形的性质及中点的坐标公式、中心对称的性质是解题的关键.

练习册系列答案
相关题目
20.把所有正奇数从小到大排列,并按如下规律分组:(1)(3,5,7)、(9,11,13,15,17),(19,21,23,25,27,29,31),…,现有等式Am=(i,j)表示正奇数m是第i组第j个数(从左往右数),如A7=(2,3),则A89=( )
| A. | (6,7) | B. | (7,8) | C. | (7,9) | D. | (6,9) |
15.若(9m+1)2=316,则正整数m的值为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
 如图,在Rt△ABC中,∠C=90°,AB的垂直平分线交BC于点E,BC=4,AC=3,则△ACE的周长为7.
如图,在Rt△ABC中,∠C=90°,AB的垂直平分线交BC于点E,BC=4,AC=3,则△ACE的周长为7.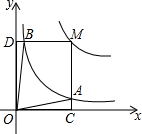 反比例函数y=$\frac{a}{x}$(a>0,a为常数)和y=$\frac{2}{x}$在第一象限内的图象如图所示,点M在y=$\frac{a}{x}$的图象上,MC⊥x轴于点C,交y=$\frac{2}{x}$的图象于点A;MD⊥y轴于点D,交y=$\frac{2}{x}$的图象于点B,当点M在y=$\frac{a}{x}$的图象上运动时,以下结论:
反比例函数y=$\frac{a}{x}$(a>0,a为常数)和y=$\frac{2}{x}$在第一象限内的图象如图所示,点M在y=$\frac{a}{x}$的图象上,MC⊥x轴于点C,交y=$\frac{2}{x}$的图象于点A;MD⊥y轴于点D,交y=$\frac{2}{x}$的图象于点B,当点M在y=$\frac{a}{x}$的图象上运动时,以下结论: