题目内容
11.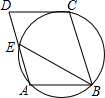 如图,在?ABCD中,过A、B、C三点的圆交AD于E,且与CD相切.若AB=4,BE=5,求DE的长.
如图,在?ABCD中,过A、B、C三点的圆交AD于E,且与CD相切.若AB=4,BE=5,求DE的长.
分析 连接CE,根据圆周角定理易知:∠BAE=∠BEC+∠EBC,而∠DCB=∠DCE+∠BCE,这两个等式中,由弦切角定理知:∠DCE=∠EBC;再由平行四边形的性质知:∠DCB=∠EAB,因此∠BEC=∠BCE,即可得BC=BE=5,即AD=5,进而可由切割线定理求DE的长.
解答 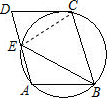 解:连接CE;
解:连接CE;
∵$\widehat{BCE}$=$\widehat{BC}$+$\widehat{CE}$,
∴∠BAE=∠EBC+∠BEC;
∵∠DCB=∠DCE+∠BCE,
由弦切角定理知:∠DCE=∠EBC,
由平行四边形的性质知:∠DCB=∠BAE,
∴∠BEC=∠BCE,即BC=BE=5,
∴AD=5,
由切割线定理知:DE=DC2÷DA=$\frac{16}{5}$.
点评 此题主要考查了平行四边形的性质、切割线定理、弦切角定理以及圆周角定理的综合应用,能够判断出△BEC是等腰三角形,是解决此题的关键.

练习册系列答案
相关题目
7.要使$\frac{x+y}{xy}$有意义,则下列说法中正确的是( )
| A. | x、y全不为零 | B. | x=0或y=0 | C. | x、y不全为零 | D. | x、y全为零 |
 把一张矩形ABCD纸片按如图方式折叠,使点A与点E重合,点C与点F重合(E、F两点均在BD上),折痕分别为BH、DG.若AB=6cm,BC=8cm,则线段FG的长为3cm.
把一张矩形ABCD纸片按如图方式折叠,使点A与点E重合,点C与点F重合(E、F两点均在BD上),折痕分别为BH、DG.若AB=6cm,BC=8cm,则线段FG的长为3cm.