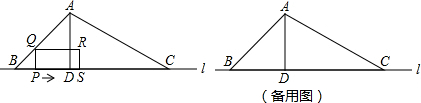题目内容
 如图,E是正方形ABCD中边CD上一点,且DE=
如图,E是正方形ABCD中边CD上一点,且DE=| 2 |
| 2 |
考点:轴对称-最短路线问题,正方形的性质
专题:
分析:根据正方形的边长和DE=
CE求出CE,再利用勾股定理列式求出BE2,作点C关于BE的对称点C′,根据垂线段最短,作C′Q⊥BC与BE的交点即为所求的点P,利用△BCE和△C′QC相似,相似三角形对应边成比例列式表示出C′Q,利用三角形的面积用CC′表示出BE,然后整理求解即可.
| 2 |
解答:解:∵四边形ABCD是正方形,
∴BC=CD=AD=3
,
∵AD=3
,DE=
CE,
∴
CE+CE=3
,
解得CE=
=6-3
,
在Rt△BCE中,BE2=BC2+CE2=(3
)2+(6-3
)2=36(2-
),
如图,作点C关于BE的对称点C′,作C′Q⊥BC与BE的交点即为所求的点P,
∵∠C′+∠BCC′=90°,
∠CBE+∠BCC′=90°,
∴∠C′=∠CBE,
又∵∠BCD=∠CQC′=90°,
∴△BCE∽△C′QC,
∴
=
,
∴C′Q=
,
∵S△BCE=
BE•
CC′=
BC•CE,
∴CC′=
=
,
∴C′Q=
,
=
=3,
即PC+PQ的最小值是3.
故答案为:3.
∴BC=CD=AD=3
| 2 |
∵AD=3
| 2 |
| 2 |
∴
| 2 |
| 2 |
解得CE=
3
| ||
|
| 2 |
在Rt△BCE中,BE2=BC2+CE2=(3
| 2 |
| 2 |
| 2 |
如图,作点C关于BE的对称点C′,作C′Q⊥BC与BE的交点即为所求的点P,

∵∠C′+∠BCC′=90°,
∠CBE+∠BCC′=90°,
∴∠C′=∠CBE,
又∵∠BCD=∠CQC′=90°,
∴△BCE∽△C′QC,
∴
| CC′ |
| BE |
| C′Q |
| BC |
∴C′Q=
3
| ||
| BE |
∵S△BCE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴CC′=
| 2BC•CE |
| BE |
2×3
| ||||
| BE |
∴C′Q=
3
| ||||||
| BE2 |
=
3×36(2-
| ||
36(2-
|
即PC+PQ的最小值是3.
故答案为:3.
点评:本题考查了轴对称确定最短路线问题,正方形的性质,相似三角形的判定与性质,三角形的面积,确定出点P的位置是解题的关键.

练习册系列答案
相关题目
已知m,n是方程x2-2
x+1=0的两根,则代数式
的值为( )
| 2 |
| m2+n2+3mn |
| A、3 | B、5 | C、9 | D、±3 |
 如图,等边三角形OAB的边长为2,将它沿AB所在的直线对折,得到△O′AB,则点O的对应点O′的坐标是( )
如图,等边三角形OAB的边长为2,将它沿AB所在的直线对折,得到△O′AB,则点O的对应点O′的坐标是( )A、(2,
| ||
| B、(4,2) | ||
C、(4,
| ||
D、(3,
|
 如图,抛物线
如图,抛物线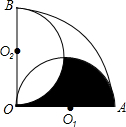 如图,扇形OAB的圆心角为90°、半径为2cm,半圆O1和半圆O2的直径分别为OA和OB,则图中阴影部分的面积为
如图,扇形OAB的圆心角为90°、半径为2cm,半圆O1和半圆O2的直径分别为OA和OB,则图中阴影部分的面积为 如图,平面直角坐标系内,若A(1,3),B(5,2),P为平面内一点,且PA的中点在x轴上,PB的中点在y轴上,则点P的坐标为
如图,平面直角坐标系内,若A(1,3),B(5,2),P为平面内一点,且PA的中点在x轴上,PB的中点在y轴上,则点P的坐标为