题目内容
9.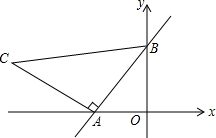 如图,在直角坐标系中,直线y=$\frac{4}{3}$x+8与x轴相交于点A,与y轴相交于点B.
如图,在直角坐标系中,直线y=$\frac{4}{3}$x+8与x轴相交于点A,与y轴相交于点B.(1)点A坐标(-6,0),点B坐标(0,8).
(2)如图,以线段AB为边在第二象限内作等腰Rt△ABC,其中∠BAC=90°,AB=AC,求直线AC的函数表达式.(请用2种方法解答).
分析 (1)将y=0代入可求得x=-6,从而可求得点A的坐标,将x=0代入求得y=8,从而可求得点B的坐标;
(2)方法1:根据相互垂直的直线的特点可知直线AC的一次项系数k=-$\frac{3}{4}$,然后利用待定系数法求得AC的解析式即可;方法2:如图所示:过点C作CD⊥x轴,垂足为D.先证明△CDA≌△AOB,于是可求得点C的坐标为(-14,6),最后利用待定系数求得AC的解析式即可.
解答 解:(1)令y=0得:$\frac{4}{3}$x+8=0,解得:x=-6,则点A的坐标为(-6,0).
将x=0代入得:y=8,则点B的坐标为(0,8).
故答案为:(-6,0);(0,8).
(2)方法1:
∵AC⊥AB,
∴直线AC与直线AB的一次项系数的乘积为-1.
∴直线AC的一次项系数k=-$\frac{3}{4}$.
设直线AC的解析式为y=$-\frac{3}{4}x+b$,将点A的坐标代入得:$-\frac{3}{4}×(-6)+b=0$,
解得:b=-$\frac{9}{2}$.
∴直线AC的函数表达式为y=$-\frac{3}{4}$x$-\frac{9}{2}$.
方法2:如图所示:过点C作CD⊥x轴,垂足为D.
∵∠CAB=90°,
∴∠CAD+∠BAO=90°.
又∵∠BAO+∠ABO=90°,
∴∠CAD=∠AB0.
在△CDA和△AOB中,
$\left\{\begin{array}{l}{∠CAD=∠AB0}\\{∠CDA=∠AOB}\\{AC=AB}\end{array}\right.$,
∴△CDA≌△AOB.
∴CD=OA=6,AD=OB=8.
∴点C的坐标为(-14,6).
设直线AC的函数表达式为y=kx+b,将点A、C的坐标代入得$\left\{\begin{array}{l}{-6k+b=0}\\{-14k+b=6}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{3}{4}}\\{b=-\frac{9}{2}}\end{array}\right.$.
∴直线AC的解析式为y=-$\frac{3}{4}x-\frac{9}{2}$.
点评 本题主要考查的是一次函数的综合应用,解答本题主要应用了待定系数法求函数的解析式、等腰直角三角形的性质、相互垂直的两条直线的解析式的特点,全等三角形的性质可判断,明确相互垂直的两条直线的一次项系数的乘积为-1以及求得点C的坐标是解题的关键.

 阅读快车系列答案
阅读快车系列答案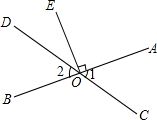 如图,∠1与∠2为对顶角,∠AOE=90°,∠BOC=5∠DOE,求∠2的度数.
如图,∠1与∠2为对顶角,∠AOE=90°,∠BOC=5∠DOE,求∠2的度数.
 如图,在平面直角坐标系中,A(0,1),B(-3,5),C(-3,1).
如图,在平面直角坐标系中,A(0,1),B(-3,5),C(-3,1).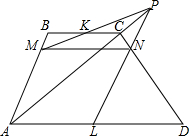 如图,在梯形ABCD的对角线AC的延长线上任取一点P,过点P与梯形两条底边的中点的连线分别交腰AB、CD于点M、N,求证:MN∥AD∥BC.
如图,在梯形ABCD的对角线AC的延长线上任取一点P,过点P与梯形两条底边的中点的连线分别交腰AB、CD于点M、N,求证:MN∥AD∥BC.