题目内容
18.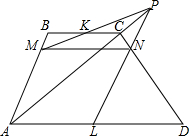 如图,在梯形ABCD的对角线AC的延长线上任取一点P,过点P与梯形两条底边的中点的连线分别交腰AB、CD于点M、N,求证:MN∥AD∥BC.
如图,在梯形ABCD的对角线AC的延长线上任取一点P,过点P与梯形两条底边的中点的连线分别交腰AB、CD于点M、N,求证:MN∥AD∥BC.
分析 要证MN∥AD∥BC,只需证明$\frac{BM}{MA}=\frac{CN}{ND}$即可.分别对△ABC和截线MKP、△ACD和截线PNL使用梅涅劳斯定理,再结合中点条件,导出所需的线段比例关系即可.
解答 证明:对于△ABC和截线MKP,由梅涅劳斯定理可得:$\frac{AM}{MB}•\frac{BK}{KC}•\frac{CP}{PA}=1$,
∵BK=CK,
∴$\frac{AM}{BM}=\frac{PA}{CP}$;
对于△ACD和截线PNL,由梅涅劳斯定理可得:$\frac{AP}{CP}•\frac{CN}{ND}•\frac{DL}{LA}=1$,
∵AL=LD,
∴$\frac{PA}{CP}=\frac{ND}{CN}$,
∴$\frac{AM}{MB}=\frac{DN}{CN}$,
∴MN∥AD∥BC.
点评 本题考查梅涅劳斯定理的基本应用,对于竞赛而言,是一道很基础的题目.熟练地识别三角形及其对应的截线是掌握好梅涅劳斯定理的基本要求.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
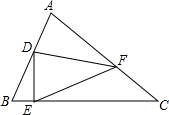 如图,在△ABC中,∠ACB=45°,D是AB边的中点,点E在BC边上,点F在AC边上,DE⊥DF,连接EF,若BE=1,EF=5,则线段AF的长为3$\sqrt{2}$.
如图,在△ABC中,∠ACB=45°,D是AB边的中点,点E在BC边上,点F在AC边上,DE⊥DF,连接EF,若BE=1,EF=5,则线段AF的长为3$\sqrt{2}$.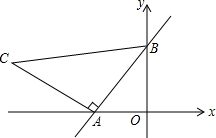 如图,在直角坐标系中,直线y=$\frac{4}{3}$x+8与x轴相交于点A,与y轴相交于点B.
如图,在直角坐标系中,直线y=$\frac{4}{3}$x+8与x轴相交于点A,与y轴相交于点B.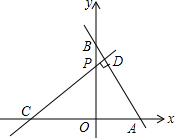 如图.在平面直角坐标系中,点C、点A为x轴上两点,OA、OC的长是方程y=x2-7x+12=0的两个根(OC>OA).点B在y轴上,CD⊥AB交y轴于点P,且CP=AB.
如图.在平面直角坐标系中,点C、点A为x轴上两点,OA、OC的长是方程y=x2-7x+12=0的两个根(OC>OA).点B在y轴上,CD⊥AB交y轴于点P,且CP=AB.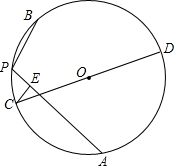 如图,PA、PB是⊙O的一条折弦,C是AB弧的中点,CD是⊙O的直径,CE⊥PA于E,求证:PD2-AD2=PA•PB.
如图,PA、PB是⊙O的一条折弦,C是AB弧的中点,CD是⊙O的直径,CE⊥PA于E,求证:PD2-AD2=PA•PB.