题目内容
6.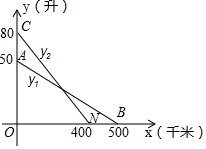 如图,线段AB、CD分别是一辆轿车的邮箱剩余油量y1(升)与另一辆客车的邮箱剩余油量y2(升)关于行驶路程x(千米)的函数图象.
如图,线段AB、CD分别是一辆轿车的邮箱剩余油量y1(升)与另一辆客车的邮箱剩余油量y2(升)关于行驶路程x(千米)的函数图象.(1)分别求出y1、y2关于x的函数解析式,并写出定义域;
(2)如果辆车同时出发,轿车的速度为100千米/小时,客车的行驶速度为80千米/小时,当邮箱剩余油量相同时,两车行驶的时间相差几分钟?
分析 (1)设轿车的邮箱剩余油量y1(升)关于行驶路程x(千米)的函数关系式为y1=k1x+b1(k1≠0),客车的邮箱剩余油量y2(升)关于行驶路程x(千米)的函数关系式为y2=k2x+b2(k2≠0),根据图形找出点的坐标利用待定系数法即可求出函数关系式;
(2)令y1=y2,求出x值,根据时间=路程÷速度即可分别算出客车和轿车行驶的时间,二者做差后即可得出结论.
解答 解:设轿车的邮箱剩余油量y1(升)关于行驶路程x(千米)的函数关系式为y1=k1x+b1(k1≠0),客车的邮箱剩余油量y2(升)关于行驶路程x(千米)的函数关系式为y2=k2x+b2(k2≠0),
将(0,50)、(500,0)代入y1=k1x+b1中,得:
$\left\{\begin{array}{l}{50={b}_{1}}\\{0=500{k}_{1}+{b}_{1}}\end{array}\right.$,解得:$\left\{\begin{array}{l}{{k}_{1}=-\frac{1}{10}}\\{{b}_{1}=50}\end{array}\right.$,
∴轿车的邮箱剩余油量y1(升)关于行驶路程x(千米)的函数关系式为y1=-$\frac{1}{10}$x+50(0≤x≤500);
同理:可求出车的邮箱剩余油量y2(升)关于行驶路程x(千米)的函数关系式为y2=-$\frac{1}{5}$x+80(0≤x≤400).
(2)当邮箱剩余油量相同时,有y1=y2,即-$\frac{1}{10}$x+50=-$\frac{1}{5}$x+80,
解得:x=300.
轿车行驶的时间为:300÷100=3(小时)=180(分钟),
客车行驶的时间为:300÷80=$\frac{15}{4}$(小时)=225(分钟),
225-180=45(分钟),
∴当邮箱剩余油量相同时,两车行驶的时间相差45分钟.
点评 本题考查了一次函数的应用以及待定系数法求函数解析式,观察函数图象找出点的坐标利用待定系数法求出函数解析式是解题的关键.