题目内容
9.已知抛物线:y=ax2+bx+c(a>0)经过A(-1,1),B(2,4)两点,顶点坐标为(m,n),有下列结论:①b<1;②c<2;③0<m<$\frac{1}{2}$;④n≤1.
则所有正确结论的序号是①②④.
分析 根据点A、B的坐标,利用待定系数法即可求出b=-a+1、c=-2a+2,结合a>0,可得出b<1、c<2,即结论①②正确;由抛物线顶点的横坐标m=-$\frac{b}{2a}$,可得出m=$\frac{1}{2}$-$\frac{1}{2a}$,即m<$\frac{1}{2}$,结论③不正确;由抛物线y=ax2+bx+c(a>0)经过A(-1,1),可得出n≤1,结论④正确.综上即可得出结论.
解答 解:∵抛物线过点A(-1,1),B(2,4),
∴$\left\{\begin{array}{l}{a-b+c=1}\\{4a+2b+c=4}\end{array}\right.$,
∴b=-a+1,c=-2a+2.
∵a>0,
∴b<1,c<2,
∴结论①②正确;
∵抛物线的顶点坐标为(m,n),
∴m=-$\frac{b}{2a}$=-$\frac{-a+1}{2a}$=$\frac{1}{2}$-$\frac{1}{2a}$,
∴m<$\frac{1}{2}$,结论③不正确;
∵抛物线y=ax2+bx+c(a>0)经过A(-1,1),顶点坐标为(m,n),
∴n≤1,结论④正确.
综上所述:正确的结论有①②④.
故答案为:①②④.
点评 本题考查了二次函数图象与系数的关系以及待定系数法求二次函数解析式,逐一分析四条结论的正误是解题的关键.

练习册系列答案
相关题目
1.在一个不透明的口袋里有红、黄、蓝三种颜色的小球,这些球除颜色外完全相同,其中有5个黄球,4个蓝球.若随机摸出一个蓝球的概率为$\frac{1}{3}$,则随机摸出一个红球的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{5}{12}$ | D. | $\frac{1}{2}$ |
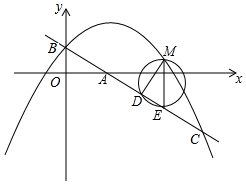 在平面直角坐标系中,直线y=-$\frac{3}{4}$x+1交y轴于点B,交x轴于点A,抛物线y=-$\frac{1}{2}$x2+bx+c经过点B,与直线y=-$\frac{3}{4}$x+1交于点C(4,-2).
在平面直角坐标系中,直线y=-$\frac{3}{4}$x+1交y轴于点B,交x轴于点A,抛物线y=-$\frac{1}{2}$x2+bx+c经过点B,与直线y=-$\frac{3}{4}$x+1交于点C(4,-2).
 如图,直线y=-$\frac{\sqrt{3}}{3}$x-$\sqrt{3}$与x,y轴分别交于点A,B,与反比例函数y=$\frac{k}{x}$的图象在第二象限交于点C,过点A作x轴的垂线交该反比例函数图象于点D.若AD=AC,则点D的坐标为(-3,2$\sqrt{3}$).
如图,直线y=-$\frac{\sqrt{3}}{3}$x-$\sqrt{3}$与x,y轴分别交于点A,B,与反比例函数y=$\frac{k}{x}$的图象在第二象限交于点C,过点A作x轴的垂线交该反比例函数图象于点D.若AD=AC,则点D的坐标为(-3,2$\sqrt{3}$).