题目内容
16.(1)在△ABC中,∠B的平分线与∠C的平分线相交于点O,如图1,小明经过探究发现:∠BOC=90°+$\frac{1}{2}$∠A,请你说明理由.(2)当∠ABC的平分线和∠ACB的外角平分线相交于点O,如图2,上面结论还成立吗?若成立说明为什么;若不成立,请你直接写出新的结论.
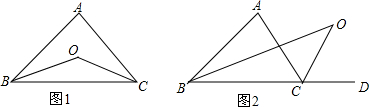
分析 (1)利用三角形的内角和定理以及角平分线的定义即可证明;
(2)利用三角形的外角等于不相邻的两个内角的和以及角平分线的定义即可求解.
解答 解:(1)在ABC中,∠BOC=180°-∠OBC-∠OCB,
∵∠B的平分线与∠C的平分线相交于点O,
∴∠OBC=$\frac{1}{2}$∠ABC,∠OCB=$\frac{1}{2}$∠ACB,
∴∠BOC=180°-∠ABC-∠ACB=180°-$\frac{1}{2}$(∠ABC+∠ACB),
∵∠ABC+∠ACB=180°-∠A,
∴∠BOC=180°-$\frac{1}{2}$(180°-∠A),
∴∠BOC=90°+$\frac{1}{2}$∠A.
(2)不成立,理由如下:
∵∠A=∠ACB-∠ABC=2∠OCD-2∠OBC=2(∠OCD-∠OBC),
∠O=∠OCD-∠OBC,
∴2∠O=∠A,
∴∠BOC=$\frac{1}{2}$∠A.
点评 本题考查的是三角形内角和定理与外角的性质,熟知三角形内角和是180°是解答此题的关键.

练习册系列答案
相关题目
5.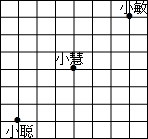 课间操时,小聪、小慧、小敏的位置如图所示,小聪对小慧说,如果我的位置用(1,1)表示,小敏的位置用(7,7)表示,那么你的位置可以表示成( )
课间操时,小聪、小慧、小敏的位置如图所示,小聪对小慧说,如果我的位置用(1,1)表示,小敏的位置用(7,7)表示,那么你的位置可以表示成( )
 课间操时,小聪、小慧、小敏的位置如图所示,小聪对小慧说,如果我的位置用(1,1)表示,小敏的位置用(7,7)表示,那么你的位置可以表示成( )
课间操时,小聪、小慧、小敏的位置如图所示,小聪对小慧说,如果我的位置用(1,1)表示,小敏的位置用(7,7)表示,那么你的位置可以表示成( )| A. | (5,4) | B. | (4,4) | C. | (3,4) | D. | (4,3) |
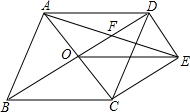 如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC,且DE=$\frac{1}{2}$AC,连接CE、OE,连接AE交OD于点F.
如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC,且DE=$\frac{1}{2}$AC,连接CE、OE,连接AE交OD于点F.
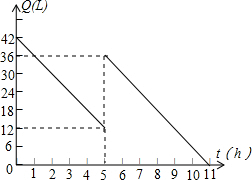 某机动车出发前油箱内有油42L,行驶若干小时后,途中在加油站加油若干升.油箱中余油量Q(L)与行驶时间t(h)之间的函数关系如图所示,根据图回答问题:
某机动车出发前油箱内有油42L,行驶若干小时后,途中在加油站加油若干升.油箱中余油量Q(L)与行驶时间t(h)之间的函数关系如图所示,根据图回答问题: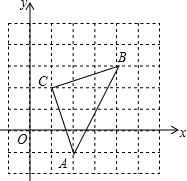 如图,直角坐标系中,△ABC的顶点都在网格点上,其中,A点坐标为(2,-1).
如图,直角坐标系中,△ABC的顶点都在网格点上,其中,A点坐标为(2,-1).