题目内容
从数列1,2,3,4,…,500中去除一些数,组成一个新数列,要求这个新数列中的任意两个数之和都不是7的倍数,则这个新数列中最大的数是( )
| A、216 | B、217 |
| C、213 | D、287 |
考点:带余除法
专题:
分析:分别列举出被7除余为1、2、3、..0的数据,进而利用余1、6,余2、5,余3、4的组间互斥,余0的组内互斥,进而求出符合题意的数据个数.
解答:解:1,2,3,4,…,500中按被7除的余数分类,
被7除余1:1、8、…498,共72个,
被7除余2:2、9、…499,共72个,
被7除余3:3、10、…500,共72个,
被7除余4:4、11、…494,共71个,
被7除余5:5、12、…495,共71个,
被7除余6:6、13、…496,共71个,
被7除余0:7、14、…497,共71个,
余1、6,余2、5,余3、4的组间互斥,余0的组内互斥,
则取余1、2、3的三组共72×3个,再取余0的组中最多个数,
综上所述,最多可取72×3+1=217个数,其中任何两个数的和都不是7的倍数.
故选:B.
被7除余1:1、8、…498,共72个,
被7除余2:2、9、…499,共72个,
被7除余3:3、10、…500,共72个,
被7除余4:4、11、…494,共71个,
被7除余5:5、12、…495,共71个,
被7除余6:6、13、…496,共71个,
被7除余0:7、14、…497,共71个,
余1、6,余2、5,余3、4的组间互斥,余0的组内互斥,
则取余1、2、3的三组共72×3个,再取余0的组中最多个数,
综上所述,最多可取72×3+1=217个数,其中任何两个数的和都不是7的倍数.
故选:B.
点评:此题主要考查了带余数的除法运算,得出符合题意的数据是解题关键.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
下列说法正确的是( )
| A、延长射线MN到点P |
| B、延长直线MN到点P |
| C、延长线段MN到点P |
| D、以上说法都正确 |
若x=-1,式子
与
的值相等,则m的值是( )
| 3x+m-1 |
| 4 |
| 2x-m+1 |
| 3 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
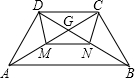 如图,在梯形ABCD中,AB∥CD,并且AB=2CD,M、N分别是对角线AC,BD的中点,设梯形ABCD的周长为L1,四边形CDMN的周长为L2,求L1:L2.
如图,在梯形ABCD中,AB∥CD,并且AB=2CD,M、N分别是对角线AC,BD的中点,设梯形ABCD的周长为L1,四边形CDMN的周长为L2,求L1:L2.