题目内容
18.在初中,我们学习过二元一次方程组,知道二元一次方程组的解法有代入消元法和加减消元法.现在我们来看一种新的方程组,二元二次方程组,含有两个未知数,且未知数的最高次数为二次的方程叫二元二次方程.将两个二元二次方程组合在一起的方程组叫二元二次方程组,二元二次方程组也可能通过二元一次方程的解法来求解,你明白了吗?那么,请解答以下问题:(1)解方程组$\left\{\begin{array}{l}{{x}^{2}+3xy+{3y}^{2}=8,…①}\\{x+2y=1,…②}\end{array}\right.$
(2)解方程组$\left\{\begin{array}{l}{{3x}^{2}+{2y}^{2}=12,…①}\\{{x}^{2}+{4y}^{2}=14,…②}\end{array}\right.$.
分析 (1)只需运用代入消元法就可解决问题;
(2)只需运用加减消元法就可解决问题.
解答 解:(1)由②得x=1-2y③,
把③代入①可得(1-2y)2+3(1-2y)y+3y2=8,
解得y1=$\frac{1+\sqrt{29}}{2}$,y2=$\frac{1-\sqrt{29}}{2}$.
当y1=$\frac{1+\sqrt{29}}{2}$时,x1=-$\sqrt{29}$;
当y2=$\frac{1-\sqrt{29}}{2}$时,x2=$\sqrt{29}$.
故原方程组的解为$\left\{\begin{array}{l}{{x}_{1}=-\sqrt{29}}\\{{y}_{1}=\frac{1+\sqrt{29}}{2}}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=\sqrt{29}}\\{{y}_{2}=\frac{1-\sqrt{29}}{2}}\end{array}\right.$.
(2)由①×2-②得,x=±$\sqrt{2}$③,
把③代入②得,y=±$\sqrt{3}$.
故原方程组的解为$\left\{\begin{array}{l}{{x}_{1}=\sqrt{2}}\\{{y}_{1}=\sqrt{3}}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=\sqrt{2}}\\{{y}_{2}=-\sqrt{3}}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{3}=-\sqrt{2}}\\{{y}_{3}=\sqrt{3}}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{4}=-\sqrt{2}}\\{{y}_{4}=-\sqrt{3}}\end{array}\right.$.
点评 本题主要考查了运用代入消元法、加减消元法解二元二次方程组,考查了运用已有的经验解决问题的能力.

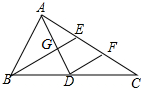 如图,在△ABC中,中线AD,BE相交于点G,过点D作DF∥BE交AC于点F,则$\frac{EF}{AC}$的值为$\frac{1}{4}$.
如图,在△ABC中,中线AD,BE相交于点G,过点D作DF∥BE交AC于点F,则$\frac{EF}{AC}$的值为$\frac{1}{4}$. 如图,O是矩形ABCD对角线的交点,∠AOB=60°,AE平分∠BAD,求∠AEO的度数.
如图,O是矩形ABCD对角线的交点,∠AOB=60°,AE平分∠BAD,求∠AEO的度数.