题目内容
8. 如图,O是矩形ABCD对角线的交点,∠AOB=60°,AE平分∠BAD,求∠AEO的度数.
如图,O是矩形ABCD对角线的交点,∠AOB=60°,AE平分∠BAD,求∠AEO的度数.
分析 根据矩形的性质可得:OB=OC,AD∥BC,∠ABC=∠BAD=90°,又由AE平分∠BAD,∠AOB=60°,求出∠OBE与∠AEB的度数,证出△OAB是等边三角形,△ABE是等腰三角形,得出△OBE是等腰三角形,求得∠OEB的度数,则问题得解.
解答 解:∵四边形ABCD是矩形,
∴AD∥BC,∠ABC=∠BAD=90°,AC=BD,OB=$\frac{1}{2}$BD,OC=$\frac{1}{2}$AC,
∴OB=OC,
∴∠OBC=∠OCB,
∵∠BOC=∠AOD=120°,
∴∠OBC=30°,
∵AE平分∠BAD,
∴∠BAE=∠EAD=45°,
∴∠AEB=∠EAD=∠BAE=45°,
∴AB=BE,
∵∠AOB=60°,
∴AB=OA=OB,
∴OB=BE,
∴∠BOE=∠BEO,
∴∠OEB=75°,
∴∠AEO=∠OEB-∠AEB=75°-45°=30°.
点评 此题考查了矩形的性质、等腰三角形的性质、等边三角形的判定与性质.熟练掌握矩形的性质,由等腰三角形的性质求出∠OEB是解决问题的关键.

练习册系列答案
相关题目
13.把直线y=3x-4沿x轴的正方向平移4个单位,得到的直线解析式为( )
| A. | y=3x | B. | y=3x-8 | C. | y=3x-16 | D. | y=3x+12 |
20.已知y与x+1成正比,当x=3时,y=12;那么当y=18时,x的值为( )
| A. | 4 | B. | -4 | C. | 5 | D. | -5 |
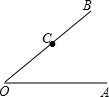 我市规划局要新建两条马路,如图所示,准备过游乐场C修一条与OA平行的马路,这条马路与∠AOB的平分线有一交点D,计划再OA边上建一个购物商场E,且使D到E最近,请利用量角器和三角板画出图形.
我市规划局要新建两条马路,如图所示,准备过游乐场C修一条与OA平行的马路,这条马路与∠AOB的平分线有一交点D,计划再OA边上建一个购物商场E,且使D到E最近,请利用量角器和三角板画出图形. 如图,平面直角坐标系中,已知y轴上有两点A、B,尺规作图作出x轴正半轴上的点P,使得∠APB最大.
如图,平面直角坐标系中,已知y轴上有两点A、B,尺规作图作出x轴正半轴上的点P,使得∠APB最大.