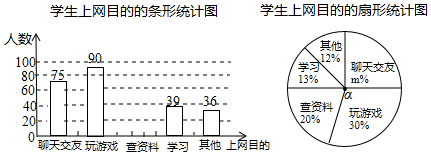
题目内容
20.在平面直角坐标系中,O为坐标原点,点A的坐标为(-3,1),将OA绕点O顺时针旋转90°得到OA′,则点A′的坐标为(1,3).分析 作AB⊥y轴于B,A′B′⊥x轴于B′.根据A点坐标可知AB、OB长度,由旋转的性质知A′B′、OB′的长度,根据A′所在象限确定其坐标.
解答 解:作AB⊥y轴于B,A′B′⊥x轴于B′.
∵A(-3,1),
∴AB=3,OB=1.
∴A′B′=3,OB′=1.
因为A′在第一象限,
∴A′(1,3).
故答案为:(1,3).
点评 此题考查了旋转的变换.熟练掌握旋转变换的性质是解题的关键.

练习册系列答案
相关题目
12.下列运算正确的是( )
| A. | 2a3÷a=6 | B. | (a+b)(a-b)=a2-b2 | C. | (ab3)2=a2b5 | D. | (a+b)2=a2+b2 |
9.下列计算正确的是( )
| A. | (a2b)3=a6b3 | B. | a3•a2=a4 | C. | b4+b4=2b8 | D. | (a-b)(b-a)=a2-b2 |
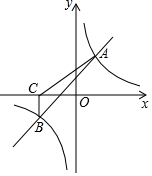 如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(2,3),
如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(2,3),