题目内容
5.(1)发现如图1,点p为线段BC上一点,∠B=∠C=90°,
填空:当∠APD=90°时,则△ABP∽△PCD;
(2)应用
填空:如图2,点E、F分别在函数$y=-\frac{4}{x}(x<0)、y=\frac{1}{x}(x>0)$的图象上,且OE⊥OF,则tan∠E=$\frac{1}{2}$;
(3)拓展.
如图3,在△ABC中,AB=AC,∠A=90°,点P为线段BC的中点,∠NPM=45°,PN交AC于点N,PM交AB于点M,连接MN,若AN=2,AC=6,求MN的长.
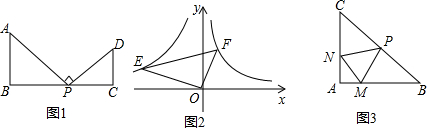
分析 (1)根据三角形内角和为180°以及平角为180°,通过角的计算可得出∠APB=∠PDC,结合∠B=∠C,即可证出△ABP∽△PCD;
(2)由(1)的结论可得出△EOE′∽△OFF′,根据相似三角形的性质结合反比例函数系数k的几何意义,即可得出$\frac{OF}{OE}$的值,再根据正切的定义即可得出结论;
(3)同(1)可求出△CNP∽△BPM,根据相似三角形的性质可求出BM的长度,进而可得出AM的长度,在Rt△AMN中,利用勾股定理可求出MN的长.
解答 解:(1)∵∠APB+∠APD+∠DPC=180°,∠APD=90°,
∴∠APB+∠DPC=90°.
又∵∠DPC+∠PDC+∠C=180°,∠C=90°,
∴∠APB=∠PDC.
∵∠B=∠C,
∴△ABP∽△PCD.
故答案为:△PCD.
(2)在图2中,过点E作EE′⊥x轴,垂足为E′,过点F作FF′⊥x轴,垂足为F′.
∵OE⊥OF,
∴△EOE′∽△OFF′,
∴$\frac{OF}{OE}$=$\sqrt{\frac{{S}_{△OFF′}}{{S}_{△EOE′}}}$.
∵点E、F分别在函数$y=-\frac{4}{x}(x<0)、y=\frac{1}{x}(x>0)$的图象上,
∴$\frac{OF}{OE}$=$\sqrt{\frac{{S}_{△OFF′}}{{S}_{△EOE′}}}$=$\sqrt{\frac{\frac{1}{2}×1}{\frac{1}{2}×|-4|}}$=$\frac{1}{2}$,
∴tan∠E=$\frac{OF}{OE}$=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
(3)∵AB=AC,∠A=90°,
∴∠C=∠B=45°,
∴∠CPN+∠CNP=180°-∠C=135°,∠BPM+∠BMP=180°-∠B=135°,
∴∠CPN+∠CNP=∠BPM+∠BMP.
∵∠NPM=45°,
∴∠CPN+∠BPM=180°-∠NPM=135°,
∴∠CNP=∠BPM.
又∵∠C=∠B,
∴△CNP∽△BPM,
∴$\frac{CN}{BP}$=$\frac{CP}{BM}$.
∵AN=2,AC=6,
∴BC=$\sqrt{2}$AC=6$\sqrt{2}$,CN=4.
∵点P为线段BC的中点,
∴CP=BP=3$\sqrt{2}$.
∴BM=$\frac{CP•BP}{CN}$=$\frac{9}{2}$,
∴AM=AB-BM=$\frac{3}{2}$.
在Rt△AMN中,AN=2,AM=$\frac{3}{2}$,∠A=90°,
∴MN=$\sqrt{A{N}^{2}+A{M}^{2}}$=$\frac{5}{2}$.
点评 本题考查了三角形内角和定理、相似三角形的判定与性质、反比例函数系数k的几何意义、正切的定义以及解直角三角形,解题的关键是:(1)通过角的计算找出∠APB=∠PDC;(2)根据相似三角形的性质结合反比例函数系数k的几何意义,找出$\frac{OF}{OE}$的值;(3)利用相似三角形的性质求出BM的长度.

 名校课堂系列答案
名校课堂系列答案 如图,数轴上有A、B、C、D四个点,其中所对应的数的绝对值最大的点是( )
如图,数轴上有A、B、C、D四个点,其中所对应的数的绝对值最大的点是( )| A. | 点A | B. | 点B | C. | 点C | D. | 点D |
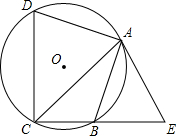 如图,已知四边形ABCD内接于⊙O,点E在CB的延长线上,连结AC、AE,∠ACB=∠BAE=45°.
如图,已知四边形ABCD内接于⊙O,点E在CB的延长线上,连结AC、AE,∠ACB=∠BAE=45°.