题目内容
20. 如图,AC是正五边形ABCDE的一条对角线,则∠ACB=36°.
如图,AC是正五边形ABCDE的一条对角线,则∠ACB=36°.
分析 由正五边形的性质得出∠B=108°,AB=CB,由等腰三角形的性质和三角形内角和定理即可得出结果.
解答 解:∵五边形ABCDE是正五边形,
∴∠B=108°,AB=CB,
∴∠ACB=(180°-108°)÷2=36°;
故答案为:36°.
点评 本题考查了正五边形的性质、等腰三角形的性质、三角形内角和定理;熟练掌握正五边形的性质,由等腰三角形的性质和三角形内角和定理求出∠ACB是解决问题的关键.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
6.已知正六边形的边长为2,则它的内切圆的半径为( )
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{3}$ |
15.已知抛物线y=ax2+bx+c(b>a>0)与x轴最多有一个交点,现有以下四个结论:
①该抛物线的对称轴在y轴左侧;
②关于x的方程ax2+bx+c+2=0无实数根;
③a-b+c≥0;
④$\frac{a+b+c}{b-a}$的最小值为3.
其中,正确结论的个数为( )
①该抛物线的对称轴在y轴左侧;
②关于x的方程ax2+bx+c+2=0无实数根;
③a-b+c≥0;
④$\frac{a+b+c}{b-a}$的最小值为3.
其中,正确结论的个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
12.一次数学测试后,某班40名学生的成绩被分为5组,第1~4组的频数分别为12、10、6、8,则第5组的频率是( )
| A. | 0.1 | B. | 0.2 | C. | 0.3 | D. | 0.4 |
9.抛物线y=x2+2x+m-1与x轴有两个不同的交点,则m的取值范围是( )
| A. | m<2 | B. | m>2 | C. | 0<m≤2 | D. | m<-2 |
 某农场拟建三间长方形种牛饲养室,饲养室的一面靠墙(墙长50m),中间用两道墙隔开(如图).已知计划中的建筑材料可建墙的总长度为48m,则这三间长方形种牛饲养室的总占地面积的最大值为144m2.
某农场拟建三间长方形种牛饲养室,饲养室的一面靠墙(墙长50m),中间用两道墙隔开(如图).已知计划中的建筑材料可建墙的总长度为48m,则这三间长方形种牛饲养室的总占地面积的最大值为144m2.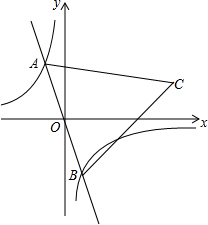 如图,在反比例函数y=-$\frac{2}{x}$的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第一象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数y=$\frac{k}{x}$的图象上运动.若tan∠CAB=2,则k的值为( )
如图,在反比例函数y=-$\frac{2}{x}$的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第一象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数y=$\frac{k}{x}$的图象上运动.若tan∠CAB=2,则k的值为( )