题目内容
16.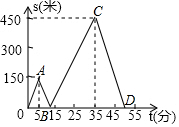 甲、乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙以50米/分的速度沿同一路线行走,设甲、乙两人相距s(米),甲行走的时间为t(分),s关于t的函数图象如图所示.
甲、乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙以50米/分的速度沿同一路线行走,设甲、乙两人相距s(米),甲行走的时间为t(分),s关于t的函数图象如图所示.(1)求乙出发多长时间后能追上甲?
(2)求直线BC的函数表达式;
(3)当甲、乙两人相距330米时,求t的值.
分析 (1)根据点A坐标的实际意义求得甲的速度,再根据相遇时甲、乙所走路程相等列方程求解可得;
(2)由(1)得出点B的坐标,待定系数法求解可得;
(3)分乙到大图书馆之前和之后两种情况,利用路程差为330列方程求解可得.
解答 解:(1)甲的速度=$\frac{150}{5}$=30米/分,
设乙走了x分钟就追上了甲,
则(50-30)x=150,
解得:x=7.5,
答:乙出发7.5分钟后能追上甲;
(2)由(1)知,点B坐标为(12.5,0)、
设BC解析式为s=kt+b,
将B(12.5,0)、C(35,450)代入,得:$\left\{\begin{array}{l}{12.5k+b=0}\\{35k+b=450}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=20}\\{b=-250}\end{array}\right.$,
∴直线BC解析式为s=20t-250;
(3)设甲行走t分钟时,甲、乙两人相距330米,
由题意50(t-5)-30t=330,解得t=29,
或30t=1500-330,解得t=39,
答:当甲、乙两人相距330米时,t的值为29或39.
点评 本题考查一次函数的应用,路程、速度、时间之间的关系等知识,解题的关键是读懂图中信息,学会用方程的思想思考问题.

练习册系列答案
相关题目
6.下列四个图形中,是中心对称图形的为( )
| A. |  | B. |  | C. |  | D. |  |
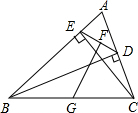 如图,BD、CE是△ABC不同边上的高,点G、F分别是BC、DE的中点,试证明GF⊥DE.
如图,BD、CE是△ABC不同边上的高,点G、F分别是BC、DE的中点,试证明GF⊥DE.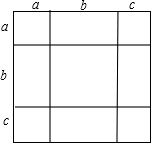 把几个图形拼成一个新的图形,再通过图形面积的计算,常常可以得到一些有用的式子,如图,是将几个面积不等的小正方形与小长方形拼成一个边长为a+b+c的正方形.
把几个图形拼成一个新的图形,再通过图形面积的计算,常常可以得到一些有用的式子,如图,是将几个面积不等的小正方形与小长方形拼成一个边长为a+b+c的正方形. 为整治城市街道的汽车超速现象,交警大队在某街道旁进行了流动测速.如图,一辆小汽车在某城市街道上直行,某一时刻刚好行驶到离车速检测仪A60m的C处,过了4s后,小汽车到达离车速检测仪A100m的B处,已知该段城市街道的限速为60km/h,请问这辆小汽车是否超速?
为整治城市街道的汽车超速现象,交警大队在某街道旁进行了流动测速.如图,一辆小汽车在某城市街道上直行,某一时刻刚好行驶到离车速检测仪A60m的C处,过了4s后,小汽车到达离车速检测仪A100m的B处,已知该段城市街道的限速为60km/h,请问这辆小汽车是否超速?