题目内容
4.先阅读下面的内容,再解决问题.例题:若m2+2mn+2n2-6n+9=0,求m和n的值.
解:∵m2+2mn+2n2-6n+9=0
∴m2+2mn+n2+n2-6n+9=0
∴(m+n)2+( n-3)2=0
∴m+n=0,n-3=0
∴m=-3,n=3
问题:
(1)若x2+2y2-2xy+4y+4=0,求x2+y2的值.
(2)已知等腰△ABC的三边长为a,b,c,其中a,b满足:a2+b2+45=12a+6b,求△ABC的周长.
分析 (1)根据完全平方公式把已知条件变形得到(x-y)2+(y+2)2=0,再根据非负数的性质求出x、y,然后把x、y的值代入计算即可;
(2)先根据完全平方公式配方,然后根据非负数的性质列式求出a、b的值,再根据等腰三角形的性质分两种情况讨论即可求解.
解答 解:(1)x2+2y2-2xy+4y+4=0,
x2-2xy+y2+y2+4y+4=0,
(x-y )2+(y+2)2=0,
∴x-y=0,y+2=0.
∴x=y=-2,
∴x2+y2=(-2)2+(-2)2=4+4=8;
(2)a2+b2+45=12a+6b,
(a-6)2+(b-3)2=0,
a-6=0,b-3=0,
解得a=6,b=3,
①若c=6 则△ABC的周长=6+6+3=15;
②若c=3,因为3+3=6,所以不能构成三角形,舍去.
故△ABC的周长是15.
点评 本题考查了配方法的应用、等腰三角形的性质、非负数的性质,利用配方法得出非负数的和是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.支付宝与“滴滴打车”联合推出优惠,“滴滴打车”一夜之间红遍大江南北,据统计,2016年“滴滴打车”账户流水总金额达到4730000000元,用科学记数法表示为( )
| A. | 4.73×108 | B. | 4.73×109 | C. | 4.73×1010 | D. | 4.73×1011 |
14. 如图所示,菱形纸片ABCD中,将纸片沿着BF折叠,使得点A落在点E,当E为CD的中点时,$\frac{BF}{AF}$=( )
如图所示,菱形纸片ABCD中,将纸片沿着BF折叠,使得点A落在点E,当E为CD的中点时,$\frac{BF}{AF}$=( )
 如图所示,菱形纸片ABCD中,将纸片沿着BF折叠,使得点A落在点E,当E为CD的中点时,$\frac{BF}{AF}$=( )
如图所示,菱形纸片ABCD中,将纸片沿着BF折叠,使得点A落在点E,当E为CD的中点时,$\frac{BF}{AF}$=( )| A. | $\frac{\sqrt{10}}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{5}{3}$ | D. | $\frac{2\sqrt{6}}{3}$ |
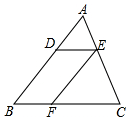 如图,已知在△ABC中,点D,E,F分别在AB,AC,BC上,DE∥BC,EF∥AB,且CF:BC=4:7,AB=14,求DB.
如图,已知在△ABC中,点D,E,F分别在AB,AC,BC上,DE∥BC,EF∥AB,且CF:BC=4:7,AB=14,求DB.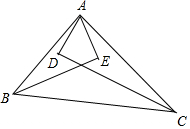 如图,已知BE,CD是△ABC的角平分线,并且AE⊥BE于点E,AD⊥DC于点D,求证:
如图,已知BE,CD是△ABC的角平分线,并且AE⊥BE于点E,AD⊥DC于点D,求证: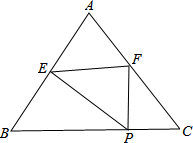 如图,已知,等腰△ABC中,AB=AC=5,BC=6,点P在BC上(与B,C不重合),作PE⊥AB,垂足是E,PF⊥BC,交AC于F,设PC=x,△PEF面积为y.
如图,已知,等腰△ABC中,AB=AC=5,BC=6,点P在BC上(与B,C不重合),作PE⊥AB,垂足是E,PF⊥BC,交AC于F,设PC=x,△PEF面积为y.
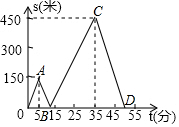 甲、乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙以50米/分的速度沿同一路线行走,设甲、乙两人相距s(米),甲行走的时间为t(分),s关于t的函数图象如图所示.
甲、乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙以50米/分的速度沿同一路线行走,设甲、乙两人相距s(米),甲行走的时间为t(分),s关于t的函数图象如图所示.