题目内容
4.某水果店出售一种水果,每只定价20元时,每周可卖出300只.试销发现以下两种情况:情况1:如果每只水果每降价1元,那么每周可多卖出25只;
情况2:如果每只水果每涨价1元,那么每周将少卖出10只.
(1)根据情况1,如何定价,才能使一周销售收入最多?
(2)如果物价局规定该种水果每只价格只能在22元~24元之间(包括22元与24元),你认为应当如何定价才能使一周销售收入最多?并说明理由.
分析 (1)根据题意可以列出相应的函数关系式,然后化为顶点式即可求得如何定价,才能使一周销售收入最多;
(2)根据题意可以列出相应的函数关系式,然后化为顶点式即可求得如何定价,才能使一周销售收入最多.
解答 解:(1)根据情况1,设当每只定价为x元时,一周销售收入为y1元,
y1=x[300+25(20-x)]=-25x2+800x=-25(x-16)2+6400,
∴当x=16时,y1有最大值,
答:当定价为16元时,一周销售收入最多;
(2)当定价为24元时,一周销售收入最多,
理由:根据情况2,设当每只定价为x元时,一周销售收入为y2元,
y2=x[300-10(x-20)]=-10x2+500x=-10(x-25)2+6250,
∴当22≤x≤24时,y2随x的增大而增大,
∴当x=24时,y2取得最大值,
即当定价为24元时,一周销售收入最多.
点评 本题考查二次函数的应用,解答本题的关键是明确题意,列出相应的函数关系式,利用二次函数的性质解答.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 填一填:如图,已知EF∥AD,∠1=∠2,∠BAC=68°.求∠AGD的度数.
填一填:如图,已知EF∥AD,∠1=∠2,∠BAC=68°.求∠AGD的度数.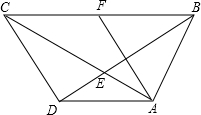 如图,在四边形ABCD中,AB=AD,AC与BD相交于点E,∠ADB=∠ACB.
如图,在四边形ABCD中,AB=AD,AC与BD相交于点E,∠ADB=∠ACB.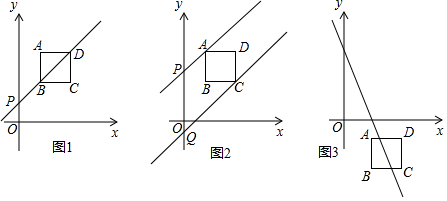
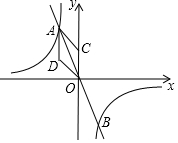 如图,反比例函数$y=\frac{k}{x}$与y=mx交于A,B两点,设点A、B的坐标分别为A(x1,y1),B(x2,y2),S=|x1y1|,且$\frac{3}{s-1}=\frac{4}{s}$,
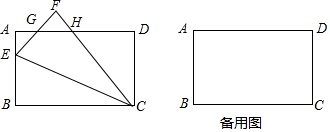
如图,反比例函数$y=\frac{k}{x}$与y=mx交于A,B两点,设点A、B的坐标分别为A(x1,y1),B(x2,y2),S=|x1y1|,且$\frac{3}{s-1}=\frac{4}{s}$,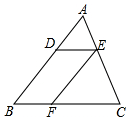 如图,已知在△ABC中,点D,E,F分别在AB,AC,BC上,DE∥BC,EF∥AB,且CF:BC=4:7,AB=14,求DB.
如图,已知在△ABC中,点D,E,F分别在AB,AC,BC上,DE∥BC,EF∥AB,且CF:BC=4:7,AB=14,求DB.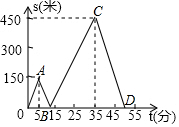 甲、乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙以50米/分的速度沿同一路线行走,设甲、乙两人相距s(米),甲行走的时间为t(分),s关于t的函数图象如图所示.
甲、乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙以50米/分的速度沿同一路线行走,设甲、乙两人相距s(米),甲行走的时间为t(分),s关于t的函数图象如图所示.