题目内容
辽宁南部素以“苹果之乡”著称.某乡组织10辆汽车装运A、B两种苹果到外地销售.按规定每辆汽车只装同一种苹果且必须装满.已知A、B两种苹果的每辆车运载量及每吨苹果获利如下表:
(1)若要求一次性运出苹果超过26吨,且一次性获利超过15000元,有哪些运输方案?
(2)哪种方案获利最大,并求出最大利润为多少元?
| 苹果品种 | A | B |
| 每辆汽车运载量(吨) | 3 | 2 |
| 每吨苹果获利(元) | 500 | 900 |
(2)哪种方案获利最大,并求出最大利润为多少元?
考点:一元一次不等式组的应用
专题:
分析:(1)设x辆汽车运A种苹果,则有(10-x)辆汽车运B种苹果,根据题意可得不等关系:①运出苹果超过26吨;②一次性获利超过15000元,根据不等关系列出不等式组,再求整数解可得答案;
(2)根据(1)中的方案,分别计算利润即可.
(2)根据(1)中的方案,分别计算利润即可.
解答:解:(1)设x辆汽车运A种苹果,则有(10-x)辆汽车运B种苹果,由题意得:
,
解得:6<x<10,
∵x为整数,
∴x=7,8,9,
运输方案:①7辆汽车运A种苹果,有3辆汽车运B种苹果;②8辆汽车运A种苹果,则有2辆汽车运B种苹果;③9辆汽车运A种苹果,则有1辆汽车运B种苹果;
(2)方案一:500×3×7+900×2×3=15900(元),
方案二:500×3×8+900×2×2=15600(元),
方案三:500×3×9+900×2×1=15300(元),
答:方案一获利最大,最大利润为15900元.
|
解得:6<x<10,
∵x为整数,
∴x=7,8,9,
运输方案:①7辆汽车运A种苹果,有3辆汽车运B种苹果;②8辆汽车运A种苹果,则有2辆汽车运B种苹果;③9辆汽车运A种苹果,则有1辆汽车运B种苹果;
(2)方案一:500×3×7+900×2×3=15900(元),
方案二:500×3×8+900×2×2=15600(元),
方案三:500×3×9+900×2×1=15300(元),
答:方案一获利最大,最大利润为15900元.
点评:此题主要考查了一元一次不等式组的应用,关键是正确理解题意,找出题目中的不等关系,列出不等式组.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
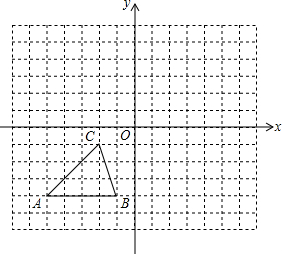 如图,方格纸中的每个小方格都是边长为1个单位的正方形,每个小正方形的顶点叫格点.已知△ABC的顶点均在格点上,在建立平面直角坐标系后,点B的坐标为l2.
如图,方格纸中的每个小方格都是边长为1个单位的正方形,每个小正方形的顶点叫格点.已知△ABC的顶点均在格点上,在建立平面直角坐标系后,点B的坐标为l2. 如图,已知点O为直线AB上一点,OE平分∠AOC,OF平分∠BOC,求∠EOF的度数.
如图,已知点O为直线AB上一点,OE平分∠AOC,OF平分∠BOC,求∠EOF的度数.