题目内容
解不等式:
(1)x>
x+1,
(2)1+
>5-
.
(1)x>
| 1 |
| 2 |
(2)1+
| x |
| 3 |
| x-2 |
| 2 |
考点:解一元一次不等式
专题:
分析:(1)移项、合并同类项,系数化成1即可求解;
(2)首先去分母,然后移项、合并同类项,系数化成1即可求解.
(2)首先去分母,然后移项、合并同类项,系数化成1即可求解.
解答:解:(1)移项,得:x-
x>1,
合并同类项,得:
x>1,
则x>2;
(2)去分母,得:6-2x>30-3(x-2),
去括号,得:6-2x>30-3x+6,
移项,得:-2x+3x>30+6-6,
合并同类项,得:x>30.
| 1 |
| 2 |
合并同类项,得:
| 1 |
| 2 |
则x>2;
(2)去分母,得:6-2x>30-3(x-2),
去括号,得:6-2x>30-3x+6,
移项,得:-2x+3x>30+6-6,
合并同类项,得:x>30.
点评:本题考查了解简单不等式的能力,解答这类题学生往往在解题时不注意移项要改变符号这一点而出错.
解不等式要依据不等式的基本性质:
(1)不等式的两边同时加上或减去同一个数或整式不等号的方向不变;
(2)不等式的两边同时乘以或除以同一个正数不等号的方向不变;
(3)不等式的两边同时乘以或除以同一个负数不等号的方向改变.
解不等式要依据不等式的基本性质:
(1)不等式的两边同时加上或减去同一个数或整式不等号的方向不变;
(2)不等式的两边同时乘以或除以同一个正数不等号的方向不变;
(3)不等式的两边同时乘以或除以同一个负数不等号的方向改变.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
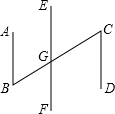 将以下各推理过程的理由填入横线内.
将以下各推理过程的理由填入横线内.