题目内容
3.在直角坐标系xOy中,对于点P(x,y)和Q(x,y′),给出如下定义:若y′=$\left\{\begin{array}{l}{y(x≥0)}\\{-y(x<0)}\end{array}\right.$,则称点Q为点P的“可控变点”.请问:若点P在函数y=-x2+16(-5≤x≤a)的图象上,其“可控变点”Q的纵坐标y′的取值范围是-16≤y′≤16,则实数a的值是4$\sqrt{2}$.分析 根据新定义,分析函数y=-x2+16在新定义下点P的“可控变点”横坐标与纵坐标的对应关系,在分析a的取值范围.
解答 解:由定义可知:
①当0≤x≤a时,y′=-x2+16,此时,抛物线y′的开口向下,故当0≤x≤a时,y′随x的增大而减小(如图)
即:-a2+16≤y′≤16,
②当-5≤x<0时,y′=x2-16,抛物线y′的开口向上,故当-5≤x<0时,y′随x的增大而减小(如图),
即:-16<y′≤9,
∵点P在函数y=-x2+16(-5≤x≤a)的图象上,其“可控变点”Q的纵坐标y′的取值范围是-16≤y′≤16,
∴-a2+16≥-16
∴a2≤32,
∴-4$\sqrt{2}$≤a≤4$\sqrt{2}$,
又∵-5≤x≤a,
∴-a=4$\sqrt{2}$,
在函数y=-x2+16图象上的点P,当a=4$\sqrt{2}$时,其“可控变点”Q的纵坐标y′的取值范围是-16≤y′≤16,
故答案为4$\sqrt{2}$
点评 本题考查了在新定义下二次函数在指定区间上的自变量与函数值之间的对应情况,解题的关键是理解在新定义下x与y′的相应区间.

练习册系列答案
相关题目

 如图,已知二次函数y=ax2+bx+c(a≠0)的图象,根据图形判断①abc>0;②a+b+c<0;③2a+b>0;④b2-4ac>4a中正确的个数有( )
如图,已知二次函数y=ax2+bx+c(a≠0)的图象,根据图形判断①abc>0;②a+b+c<0;③2a+b>0;④b2-4ac>4a中正确的个数有( ) 如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于(1,3),B(3,n)两点.
如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于(1,3),B(3,n)两点. 如图,在平行四边形ABCD中,E、F为对角线AC上两点,且AE=CF,请你从图中找出一对全等三角形,并给予证明.
如图,在平行四边形ABCD中,E、F为对角线AC上两点,且AE=CF,请你从图中找出一对全等三角形,并给予证明.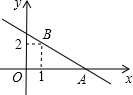 如图,直线y=kx+b经过点A(3,0),B(1,2),则关于x的不等式0≤kx+b<2x的解集为1<x≤3.
如图,直线y=kx+b经过点A(3,0),B(1,2),则关于x的不等式0≤kx+b<2x的解集为1<x≤3. 在下列括号内,填上推理的根据.
在下列括号内,填上推理的根据.