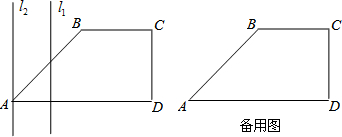
题目内容
在△ABC中,BA=BC,BD为△ABC的中线,△ABC的角平分线AE交BD于点F,过点C作AB的平行线交AE的延长线于点G.
(1)如图1,若∠ABC=60°,请直接写出线段AF,EG间的数量关系: ;
(2)如图2,若∠ABC=90°,求证:EG=2AF;
(3)在(2)的条件下,如图3,在∠FAC的外部作∠CAH,使∠CAH=
∠FAC,过点B作BM∥AC交AG于点M,点N在AH上,连接MN,BN,若∠BMN与∠EAH互余,△ABC的面积为18,求BN的长.

(1)如图1,若∠ABC=60°,请直接写出线段AF,EG间的数量关系:
(2)如图2,若∠ABC=90°,求证:EG=2AF;
(3)在(2)的条件下,如图3,在∠FAC的外部作∠CAH,使∠CAH=
| 1 |
| 3 |

考点:全等三角形的判定与性质,等边三角形的判定与性质
专题:
分析:(1)先判断出△ABC是等边三角形,设DF=a,表示出AF、EF,根据两直线平行,内错角相等求出∠G=∠CAE=30°,表示出GE,然后相比即可;
(2)取EG的中点P,连接CF、CP,根据角平分线的定义求出∠BAE=∠FAC=22.5°,根据等腰直角三角形的对称性可得AF=CF,然后求出∠CFP=45°,再求出∠ECG=90°,根据直角三角形斜边上的中线等于斜边的一半可得CP=GP=
EG,根据两直线平行,内错角相等可得∠G=∠BAE=22.5°,再求出∠CPF=45°,根据等角对等边可得CF=CP,从而得到AF=CP,AF=
EG,整理即可得证;
(3)过点B作BK⊥AM于K,过点M作ML⊥AH于H,先求出∠EAH=30°,根据直角三角形两锐角互余求出∠AML=∠BMN=60°,然后求出∠BMK=∠NML,再求出∠BAE=∠BME=22.5°,根据等角对等边可得AB=BM,根据等腰三角形三线合一的性质可得MK=
AM,根据直角三角形斜边上的中线等于斜边的一半可得ML=
AM,从而得到MK=ML,再利用“角边角”证明△BMK和△NML全等,根据全等三角形对应边相等可得MN=BM,再根据等腰直角三角形的面积求出AB,再判断出△BMN是等边三角形,然后求解即可.
(2)取EG的中点P,连接CF、CP,根据角平分线的定义求出∠BAE=∠FAC=22.5°,根据等腰直角三角形的对称性可得AF=CF,然后求出∠CFP=45°,再求出∠ECG=90°,根据直角三角形斜边上的中线等于斜边的一半可得CP=GP=
| 1 |
| 2 |
| 1 |
| 2 |
(3)过点B作BK⊥AM于K,过点M作ML⊥AH于H,先求出∠EAH=30°,根据直角三角形两锐角互余求出∠AML=∠BMN=60°,然后求出∠BMK=∠NML,再求出∠BAE=∠BME=22.5°,根据等角对等边可得AB=BM,根据等腰三角形三线合一的性质可得MK=
| 1 |
| 2 |
| 1 |
| 2 |
解答:(1)解:∵BA=BC,∠ABC=60°,
∴△ABC是等边三角形,
设DF=a,
∵BD为△ABC的中线,AE为△ABC的角平分线,
∴AF=2a,EF=a,
∵CG∥AB,
∴∠G=∠CAE=∠CAE=30°,
∴GE=AE=AF+EF=2a+a=3a,
∴AF=
EG;
故答案为:AF=
EG.
(2)证明:取EG的中点P,连接CF、CP,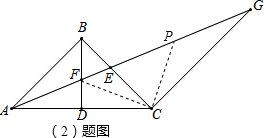
∵BA=BC,∠ABC=90°,
∴△ABC是等腰直角三角形,
∴AF=CF,
∵AF是△ABC的角平分线,
∴∠BAE=∠FAC=22.5°,
∴∠CFP=45°,
∵CG∥AB,
∴∠ECG=∠ABC=90°,
∴CP=GP=
EG,
∵CG∥AB,
∴∠G=∠BAE=22.5°,
∴∠CPF=45°,
∴CF=CP,
∴AF=
EG,
故EG=2AF;
(3)解:过点B作BK⊥AM于K,过点M作ML⊥AH于H,
∵∠CAH=
∠FAC,
∴∠EAH=22.5°+
×22.5°=30°,
∴∠AML=90°-30°=60°,
∵∠BMN与∠EAH互余,
∴∠BMN=90°-30°=60°,
∴∠BMK=∠NML,
∵AE是△ABC的平分线,CG∥AB,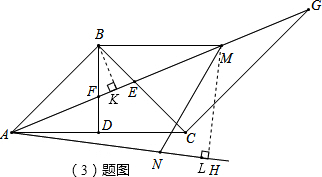
∴∠BAE=∠BME=
×45°=22.5°,
∴AB=BM,
∴MK=
AM,
∵∠MAH=30°,ML⊥AH,
∴MH=
AM,
∴MK=ML,
在△BMK和△NML中,
,
∴△BMK≌△NML(ASA),
∴MN=BM,
∴MN=AB,
∵△ABC的面积为18,
∴
AB2=18,
∴AB=6,
∵∠BMN=60°,BM=MN,
∴△BMN是等边三角形,
∴BN=MN=6.
∴△ABC是等边三角形,
设DF=a,
∵BD为△ABC的中线,AE为△ABC的角平分线,
∴AF=2a,EF=a,
∵CG∥AB,
∴∠G=∠CAE=∠CAE=30°,
∴GE=AE=AF+EF=2a+a=3a,
∴AF=
| 3 |
| 2 |
故答案为:AF=
| 3 |
| 2 |
(2)证明:取EG的中点P,连接CF、CP,

∵BA=BC,∠ABC=90°,
∴△ABC是等腰直角三角形,
∴AF=CF,
∵AF是△ABC的角平分线,
∴∠BAE=∠FAC=22.5°,
∴∠CFP=45°,
∵CG∥AB,
∴∠ECG=∠ABC=90°,
∴CP=GP=
| 1 |
| 2 |
∵CG∥AB,
∴∠G=∠BAE=22.5°,
∴∠CPF=45°,
∴CF=CP,
∴AF=
| 1 |
| 2 |
故EG=2AF;
(3)解:过点B作BK⊥AM于K,过点M作ML⊥AH于H,
∵∠CAH=
| 1 |
| 3 |
∴∠EAH=22.5°+
| 1 |
| 3 |
∴∠AML=90°-30°=60°,
∵∠BMN与∠EAH互余,
∴∠BMN=90°-30°=60°,
∴∠BMK=∠NML,
∵AE是△ABC的平分线,CG∥AB,

∴∠BAE=∠BME=
| 1 |
| 2 |
∴AB=BM,
∴MK=
| 1 |
| 2 |
∵∠MAH=30°,ML⊥AH,
∴MH=
| 1 |
| 2 |
∴MK=ML,
在△BMK和△NML中,
|
∴△BMK≌△NML(ASA),
∴MN=BM,
∴MN=AB,
∵△ABC的面积为18,
∴
| 1 |
| 2 |
∴AB=6,
∵∠BMN=60°,BM=MN,
∴△BMN是等边三角形,
∴BN=MN=6.
点评:本题考查了全等三角形的判定与性质,等边三角形的性质,等腰三角形的判定与性质,直角三角形30°角所对的直角边等于斜边的一半的性质,平行线的性质,熟记各性质并理解题目信息是解题的关键,难点在于作辅助线构造出全等三角形和等腰三角形.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目