题目内容
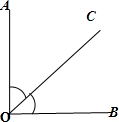
OC把∠AOB分成两部分,且有以下两个等式成立:①∠AOC=
×90°+
∠BOC;②∠BOC=
×180°-
∠AOC,问:
(1)OA与OB的位置关系怎样?
(2)OC是否为∠AOB的平分线?并写出判断的理由.
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
(1)OA与OB的位置关系怎样?
(2)OC是否为∠AOB的平分线?并写出判断的理由.
考点:角的计算,角平分线的定义
专题:常规题型
分析:将②代入①得:∠AOC=45°,然后将∠AOC=45°代入②得∠BOC=45°,从而得出OA与OB的位置关系为互为垂直,OC为∠AOB的平分线.
解答:解:(1)OA⊥OB,
将②∠BOC=
×180°-
∠AOC,代入①∠AOC=
×90°+
∠BOC得:
∠AOC=
×90°+
(
×180°-
∠AOC),
∠AOC=
×90°+20°-
∠AOC,
∠AOC=50°,
∴∠AOC=50°÷
=45°,
将∠AOC=45°代入②得,
∠BOC=
×180°-
×45°
=60°-15°
=45°.
∵∠AOB=∠AOC+∠BOC=45°+45°=90°,
∴OA⊥OB.
(2)OC是∠AOB的平分线,
由(1)知,∠AOC=45°,∠BOC=45°,
∴∠AOC=∠BOC,
∴OC是∠AOB的平分线(角平分线的定义).
将②∠BOC=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
∠AOC=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
∠AOC=
| 1 |
| 3 |
| 1 |
| 9 |
| 10 |
| 9 |
∴∠AOC=50°÷
| 10 |
| 9 |
将∠AOC=45°代入②得,
∠BOC=
| 1 |
| 3 |
| 1 |
| 3 |
=60°-15°
=45°.
∵∠AOB=∠AOC+∠BOC=45°+45°=90°,
∴OA⊥OB.
(2)OC是∠AOB的平分线,
由(1)知,∠AOC=45°,∠BOC=45°,
∴∠AOC=∠BOC,
∴OC是∠AOB的平分线(角平分线的定义).

点评:本题考查了角的计算,解题的关键是:将两式进行等量代换即可.

练习册系列答案
相关题目
在数轴上表示不等式x+2≥0的解集,正确的是( )
A、 |
B、 |
C、 |
D、 |
 (1)如图,△ABC是等边三角形,过它的三个顶点分别作对边的平行线,得到一个新的三角形DEF,△DEF是等边三角形吗?你还能找到其他的等边三角形吗?点A,B,C分别是EF,ED,FD的中点吗?请证明你的结论.
(1)如图,△ABC是等边三角形,过它的三个顶点分别作对边的平行线,得到一个新的三角形DEF,△DEF是等边三角形吗?你还能找到其他的等边三角形吗?点A,B,C分别是EF,ED,FD的中点吗?请证明你的结论.