题目内容
如图,在直角梯形ABCD中,∠D=∠C=90°,BC=CD=4cm,∠BAD=45°,过点A有两条动直线l1和l2从点A出发,且l1⊥AD,l2⊥AD,l1以1cm/s的速度从点A出发沿AD方向移动,经过4秒后,l2以2cm/s的速度沿AD方向移动,设l1,l2与梯形的边围成的图形的面积为S,设l1移动的时间为t.
(1)AD= ;
(2)求S与t之间的函数关系式及S的最大值.
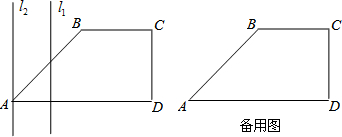
(1)AD=
(2)求S与t之间的函数关系式及S的最大值.

考点:相似形综合题
专题:
分析:(1)过点B作BE⊥AD,根据所给出的条件得出四边形BCDE是矩形,从而求出BE、DE,再根据∠BAD=45°,求出AE的值,即可得出答案,
(2)当0<t≤2时,设l1交AB于点F,交AD于点G,l2交AB于点M,交AD于点N,根据l1以1cm/s的速度从点A出发沿AD方向移动,l1移动的时间为t,求出AG、FG,再根据经过4秒后,l2以2cm/s的速度沿AD方向移动,求出AN、MN=2(t-4),从而求出NG,再根据梯形面积公式即可得出l1,l2与梯形的边围成的图形的面积为S=
[(2t-8)+t](8-t)然后进行整理,当2<t≤4时,设l1交AB于点F,交AD于点G,l2交AB于点M,交AD于点N,求出NG,再求出FG,最后根据矩形的面积公式列式计算即可.
(2)当0<t≤2时,设l1交AB于点F,交AD于点G,l2交AB于点M,交AD于点N,根据l1以1cm/s的速度从点A出发沿AD方向移动,l1移动的时间为t,求出AG、FG,再根据经过4秒后,l2以2cm/s的速度沿AD方向移动,求出AN、MN=2(t-4),从而求出NG,再根据梯形面积公式即可得出l1,l2与梯形的边围成的图形的面积为S=
| 1 |
| 2 |
解答: 解:(1)过点B作BE⊥AD,垂足为点E,
解:(1)过点B作BE⊥AD,垂足为点E,
∵∠D=∠C=90°,
∴四边形BCDE是矩形,
∴BE=CD=4,DE=BC=4,
∵∠BAD=45°,
∴AE=BE=4,
∴AD=4+4=8(cm),
故答案为;8cm,
(2)当0<t≤2时,如图设l1交AB于点F,交AD于点G,l2交AB于点M,交AD于点N,
∵l1以1cm/s的速度从点A出发沿AD方向移动,l1移动的时间为t,
∴AG=FG=tcm,
∵经过4秒后,l2以2cm/s的速度沿AD方向移动,
∴AN=MN=2(t-4)=(2t-8)cm,
∴NG=AG-AN=t-(2t-8)=(8-t)cm,
∴l1,l2与梯形的边围成的图形的面积为S=
[(2t-8)+t](8-t)=(-
t2+16t-32)=(cm2),
∴S的最大值=
cm2,
当2<t≤4时,如图设l1交AB于点F,交AD于点G,l2交AB于点M,交AD于点N,
则NG=AG-AN=t-(2t-8)=(8-t)cm,
∵FG=CD=4cm,
∴l1,l2与梯形的边围成的图形的面积为S=NG•FG=4(8-t)=(32-4t)(cm2)
∴S的最大值=32(cm2).
 解:(1)过点B作BE⊥AD,垂足为点E,
解:(1)过点B作BE⊥AD,垂足为点E,∵∠D=∠C=90°,
∴四边形BCDE是矩形,
∴BE=CD=4,DE=BC=4,
∵∠BAD=45°,
∴AE=BE=4,
∴AD=4+4=8(cm),

故答案为;8cm,
(2)当0<t≤2时,如图设l1交AB于点F,交AD于点G,l2交AB于点M,交AD于点N,
∵l1以1cm/s的速度从点A出发沿AD方向移动,l1移动的时间为t,
∴AG=FG=tcm,
∵经过4秒后,l2以2cm/s的速度沿AD方向移动,
∴AN=MN=2(t-4)=(2t-8)cm,

∴NG=AG-AN=t-(2t-8)=(8-t)cm,
∴l1,l2与梯形的边围成的图形的面积为S=
| 1 |
| 2 |
| 3 |
| 2 |
∴S的最大值=
| 32 |
| 3 |
当2<t≤4时,如图设l1交AB于点F,交AD于点G,l2交AB于点M,交AD于点N,
则NG=AG-AN=t-(2t-8)=(8-t)cm,
∵FG=CD=4cm,
∴l1,l2与梯形的边围成的图形的面积为S=NG•FG=4(8-t)=(32-4t)(cm2)
∴S的最大值=32(cm2).
点评:此题考查了相似形综合,用到的知识点是梯形矩形的面积、等腰直角三角形的性质、二次函数的最值,关键是根据题意画出图形,注意分两种情况.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
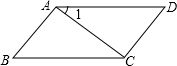 如图,∠1=25°,∠B=65°,AB⊥AC.
如图,∠1=25°,∠B=65°,AB⊥AC.