题目内容
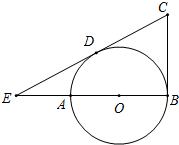 如图,AB是⊙O的直径,BC切⊙O于B,CD切⊙O于D,交AB的延长线于E.若BC=6,EB=8,求EA.
如图,AB是⊙O的直径,BC切⊙O于B,CD切⊙O于D,交AB的延长线于E.若BC=6,EB=8,求EA.考点:切线的性质
专题:计算题
分析:连结OD,如图,根据切线的性质得∠CBA=90°,可根据勾股定理计算出CE=10,再根据切线的性质和切线长定理得CD=CB=6,OD⊥CE,则DE=CE-CD=4,然后证明Rt△EOD≌Rt△ECB,利用相似比可计算出OD=3,OE=5,所以AE=OE-OA=2.
解答: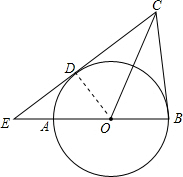 解:连结OD,如图,
解:连结OD,如图,
∵BC切⊙O于B,
∴BC⊥AB,
∴∠CBA=90°,
在Rt△BCE中,∵BC=6,EB=8,
∴CE=
=10,
∵CE切⊙O于D,
∴CD=CB=6,OD⊥CE,
∴DE=CE-CD=4,
∵∠OEA=∠CEB,
∴Rt△EOD≌Rt△ECB,
∴
=
=
,即
=
=
,
∴OD=3,OE=5,
∴AE=OE-OA=5-3=2.
 解:连结OD,如图,
解:连结OD,如图,∵BC切⊙O于B,
∴BC⊥AB,
∴∠CBA=90°,
在Rt△BCE中,∵BC=6,EB=8,
∴CE=
| BC2+BE2 |
∵CE切⊙O于D,
∴CD=CB=6,OD⊥CE,
∴DE=CE-CD=4,
∵∠OEA=∠CEB,
∴Rt△EOD≌Rt△ECB,
∴
| OD |
| BC |
| DE |
| BE |
| OE |
| CE |
| OD |
| 6 |
| 4 |
| 8 |
| OE |
| 10 |
∴OD=3,OE=5,
∴AE=OE-OA=5-3=2.
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了勾股定理、相似三角形的判定与性质.

练习册系列答案
相关题目
某小组计划做一批“中国结”,如果每人做5个,那么比计划多了9个.如果每人做4个,那么比计划少15个,若用方程描述其中数量之间的相等关系,设他们计划做x个“中国结”,则得方程( )
| A、5x-9=4x+15 | ||||
| B、5x+9=4x-15 | ||||
C、
| ||||
D、
|
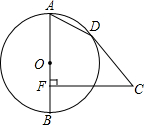 如图,AB是⊙O的直径,CD切⊙O于D,CF⊥AB于F,若tan∠A=2,求sin∠DCF的值.
如图,AB是⊙O的直径,CD切⊙O于D,CF⊥AB于F,若tan∠A=2,求sin∠DCF的值. 如图,AB是⊙O的直径,CD切⊙O于C,OD⊥AB交AC于E,tan∠DEC=3,求sin∠D的值.
如图,AB是⊙O的直径,CD切⊙O于C,OD⊥AB交AC于E,tan∠DEC=3,求sin∠D的值.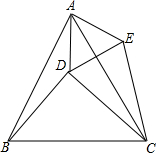 如图,△ABC是等边三角形,△BDC是等腰直角三角形,∠BDC=90°,连接AD,以AD为边作等边△ADE,连接CE.
如图,△ABC是等边三角形,△BDC是等腰直角三角形,∠BDC=90°,连接AD,以AD为边作等边△ADE,连接CE.