题目内容
14．已知|a-b-1|+（b-2a+c）2+|2c-b|=0，则a=-3，b=-4，c=-2．分析 利用非负数的性质列出三元一次方程组，求出方程组的解即可得到a，b，c的值．
解答 解：∵|a-b-1|+（b-2a+c）2+|2c-b|=0，
∴$\left\{\begin{array}{l}{a-b=1}\\{b-2a+c=0}\\{2c-b=0}\end{array}\right.$，
解得：a=-3，b=-4，c=-2．
故答案为：-3；-4；-2
点评 此题考查了解三元一次方程组，以及非负数的性质，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
4．关于x，y的方程组$\left\{\begin{array}{l}x+py=0\\ x+y=3\end{array}\right.$的解是$\left\{\begin{array}{l}x=1\\ y=▲\end{array}$，其中y的值被盖住了，不过仍能求出p，则p的值是（ ）
| A． | -$\frac{1}{2}$ | B． | $\frac{1}{2}$ | C． | -$\frac{1}{4}$ | D． | $\frac{1}{4}$ |
5．某超市设计了一种促销活动：在一个不透明的箱子里放有4个相同的小球，球上分别标有“0元”、“5元”、“10元”、“20元”的字样．规定：顾客在本超市一次性消费满200元，就可以在箱子里先后摸出两个小球（每一次摸出后不放回），并根据两个小球所标总金额换取等值的购物券．某顾客刚好消费200元，则该顾客所获得购物券的金额不低于20元的概率为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{3}{4}$ | C． | $\frac{1}{3}$ | D． | $\frac{2}{3}$ |
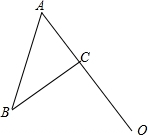如图，在△ABC中，AB=5，BC=4，AC=3，点O在AC的延长线上，且OC=4．
如图，A，B两处加工厂需从设在x轴上的C贷站和y轴上的D货站来回调运货物，当C，D建于何处时，AB+BC+CD+DA的路程最短？
3．如果x2-px+q=（x+a）（x+b），那么p等于（ ）
| A． | ab | B． | a+b | C． | -ab | D． | -（a+b） |