题目内容
19.已知x2-6x+9+|y+1|=0,求(x+2y)2(x-2y)2-(x-2y)(x2+4y2)(x+2y)的值.分析 首先利用绝对值以及偶次方的性质得出x,y的值,再将原式化简求出答案.
解答 解:∵x2-6x+9+|y+1|=0,
∴(x-3)2+|y+1|=0,
解得:x=3,y=-1,
(x+2y)2(x-2y)2-(x-2y)(x2+4y2)(x+2y)
=(x-2y)(x+2y)[(x+2y)(x-2y)-(x2+4y2)]
=(x2-4y2)(x2-4y2-x2-4y2)
=-8y2(x2-4y2),
则将x=3,y=-1代入得:
原式=-8×(-1)2[32-4×(-1)2]
=-8×(9-4)
=-40.
点评 此题主要考查了整式的混合运算,正确利用乘法公式计算是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.若点(-1,y1),(-2,y2),(2,y3)在反比例函数$y=-\frac{{{k^2}+1}}{x}$图象上,则下列结论正确的是( )
| A. | y1>y2>y3 | B. | y2>y1>y3 | C. | y3>y1>y2 | D. | y3>y2>y1 |
19.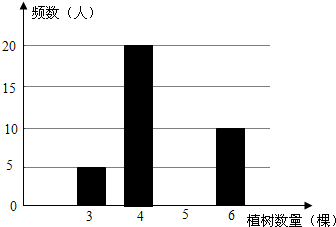 学校组织师生开展植树造林活动,为了了解全校4000名学生的情况,随机抽样调查50名学生的植树情况,制成如下统计表和条形统计图(均不完整).
学校组织师生开展植树造林活动,为了了解全校4000名学生的情况,随机抽样调查50名学生的植树情况,制成如下统计表和条形统计图(均不完整).
(1)将统计表和条形统计图补充完整;
(2)求抽样的50名学生植树数量的平均数;
(3)根据抽样数据,估计该校4000名学生的植树数量.
 学校组织师生开展植树造林活动,为了了解全校4000名学生的情况,随机抽样调查50名学生的植树情况,制成如下统计表和条形统计图(均不完整).
学校组织师生开展植树造林活动,为了了解全校4000名学生的情况,随机抽样调查50名学生的植树情况,制成如下统计表和条形统计图(均不完整).(1)将统计表和条形统计图补充完整;
(2)求抽样的50名学生植树数量的平均数;
(3)根据抽样数据,估计该校4000名学生的植树数量.
| 植树数量 (棵) | 频数 (人) | 频率 |
| 3 | 5 | 0.1 |
| 4 | 20 | 0.4 |
| 5 | 15 | 0.3 |
| 6 | 10 | 0.2 |
| 合计 | 50 | 1 |
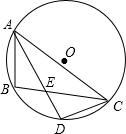 如图,AB,AC是⊙O弦,∠BAC的角平分线交⊙O于点D,AD与BC交于点E,若DE=2cm,AE=8cm,则DC=2$\sqrt{5}$cm.
如图,AB,AC是⊙O弦,∠BAC的角平分线交⊙O于点D,AD与BC交于点E,若DE=2cm,AE=8cm,则DC=2$\sqrt{5}$cm.